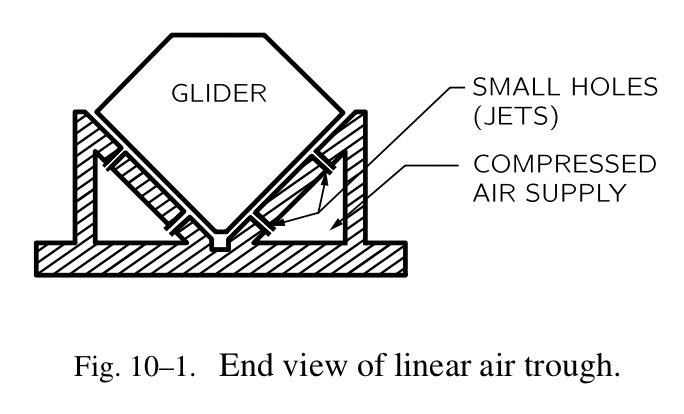
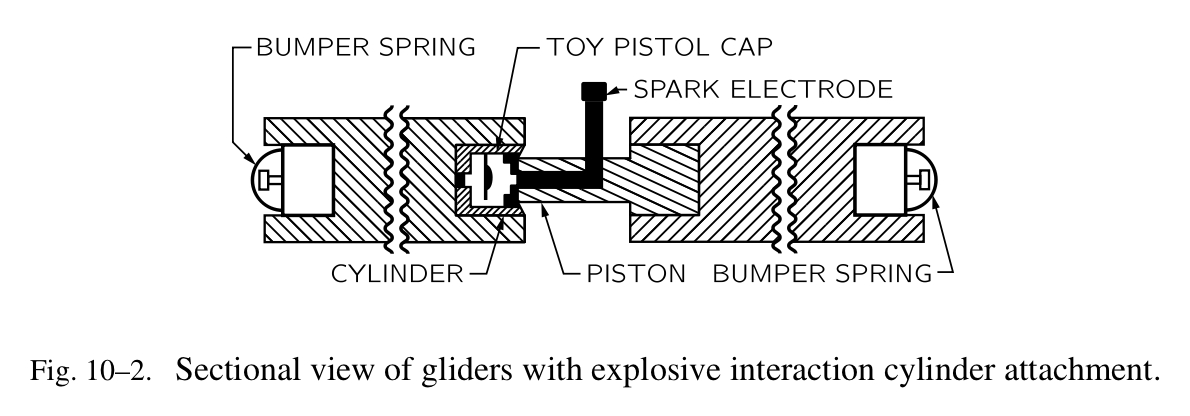
我们可以用实验验证上章的假设:首先,两个相等质量的静止物体,它们被一个爆炸分开,它们会以相同的速率运动,其次,如果两个相等质量的物体,它们以相同的速率相撞在一起,它们会静止。我们有一个超级棒的发明——叫做空气槽,它避免了摩擦力,该力一直烦扰着伽利略(Fig.10-1)。他无法通过滑动物体来做实验,因为它们不能自由地滑动,但是通过施加一些魔力,我们就可以避免摩擦力。我们的物体无障碍移动,始终保持一个恒定的速度,正如伽利略所宣扬的。它是通过让空气支撑物体来实现的。因为空气有非常低的摩擦力,一个物体会以恒定的速度滑动,当没有阻力的话。首先,我们使用两个滑块,它们被仔细地制造,拥有相同的重量,或者质量(它们的重量被测量出来,但是我们知道重量与质量成正比),并且在一个封闭的圆柱体里,在它们之间放置一个小的爆破帽(explosive cap)(Fig.10-2)。我们应该让位于轨道中间点的滑块从静止启动,并且通过使用电子火花引爆它(explosive cap),让它们强制分离。会发生什么呢?如果在它们飞出去的时候速率相等,它们应该在同一时间到达轨道末端。在碰到终端后,它们会以相反的速度折返,并且聚在一起,停在中点(它们开始的地方)。这是一个不错的测试;在它被完成后,结果正如 Fig.10-3 所描述的。
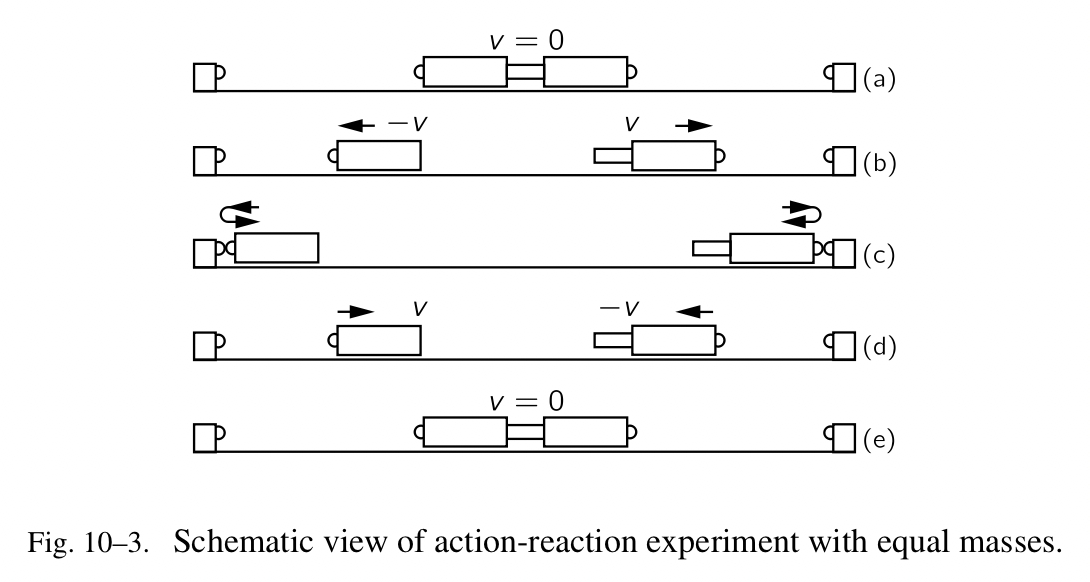
接下来我们想搞明白的是在一个不那么简单的情形中会发生什么。假设我们有两个相等的质量,一个以速度 v 移动,另一个静止,它们相撞在一起;将会发生什么?当我们完成时,有一个质量 2m,它以一个未知的速度移动。什么速度?这就是问题所在。为了寻找答案,我们做出假设,如果我们坐在一辆汽车里,物理会看起来一致,正如我们静止的时候。我们从这条知识出发,两个相等的质量以相等的速率 v 沿着相反的方向运动,当它们相撞时会停止。假设在它发生的同时,我们坐在一辆汽车里,速度是 -v ,那么它看起来会是什么样的?因为我们伴随着两个质量之一,它们相向运动,有一个在我们看来是零的速度,另一个,带着相反的速度 v,看起来似乎是以速度 2v 朝向我们(Fig.10-4)。最终,在碰撞之后合并的质量,好像传递了速度 v 。我们因此总结一个带着速度 2v 的物体,冲撞一个处于静止的相等的物体,将会带着速度 v 结束,或者完全一样的数学表达,一个伴随着速度 v 的物体与一个静止的物体冲撞在一起,将会产生一个以速度 v/2 移动的物体。注意,在冲撞之前我们把质量乘以速度,再把它们都加起来, $mv+0$ ,我们会得到相同的答案,正如在冲撞之后我们把质量乘以速度,2m 乘以 v/2 。它让我们了解一个带着速度 v 的物体冲击一个静止的会发生什么。
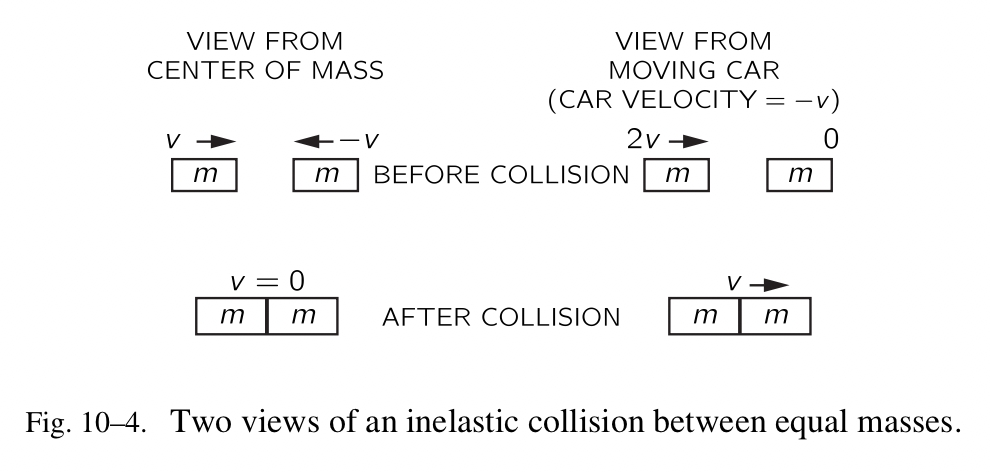
以完全相同的方式我们可以推导,当拥有任意两个速度的相等物体彼此冲撞时会发生什么。
如果我们有两个相等的物体,它们的速度分别是 $v_1$ 和 $v_2$ ,它们冲撞在一起,那么在冲撞之后它们的速度 v 是什么?我们再次坐在一个汽车里,速度是 $v_2$ ,所以一个物体看起来是静止的。另一个的速度看起来是 $v_1-v_2$ ,我们得到了一个与之前一样的示例。当所有的完成时,相对于汽车(我们乘坐的)它们将会以 $\frac{1}{2}(v_1-v_2)$ 移动。那么在地面上真实的速率是多少?

$v=\frac{1}{2}(v_1-v_2)+v_2$ 或者 $v=\frac{1}{2}(v_1+v_2)$ 。我们再次注意到:
\[mv_1+mv_2=2m(v_1+v_2)\frac{1}{2}\]因此使用这个原理,我们可以分析任意种类的冲撞——两个相等质量的物体彼此撞在一起。实际上,虽然我们只是在一个维度上,但是我们可以通过想象我们所乘坐的汽车沿着某个倾斜的方向,从而搞明白很多更加复杂的冲撞。原理是一样的,但是细节变复杂了。
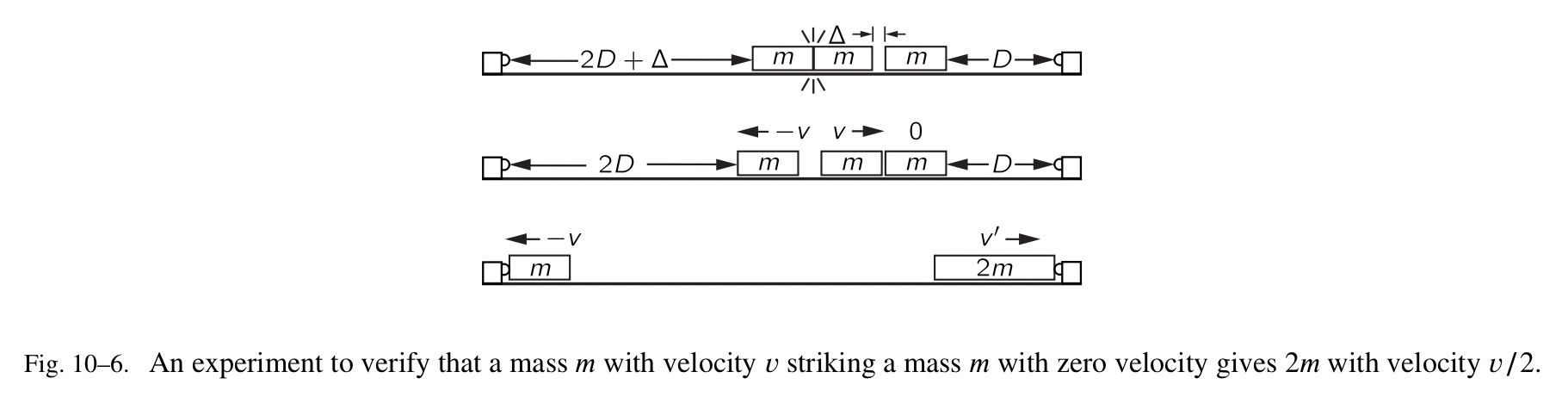
为了测试一个以速度 v 移动的物体,与一个静止的相等的物体冲撞,是否会产生一个以速度 v/2 移动的物体,我们也许可以使用空气槽设备执行下面的实验。我们在槽上放置了三个相等质量的物体,其中两个由可爆炸的圆柱体设备连接,第三个靠的非常的近,但是会分开一点点,有一个粘接杆(sticky bumper),可以粘接与之相撞的物体。现在,在爆炸之后的那个时刻,我们有两个质量为 m 的物体,它们以相等且相反的速度 v 移动。在那个时刻之后,它们中的一个与第三个物体碰撞,然后产生了一个质量为 2m 的物体,我们相信,它的速度是 v/2 。我们怎么测试它是否真的是 v/2 ?通过在槽轨上分配质量(物体)的初始位置,让它们到终端的距离不相等,比例为 2:1 。因此我们的第一个质量,以速度 v 持续移动,它应该会跑 2 倍的距离,相较于两个连在一起的(允许第二个物体在与第三个物体碰撞之前跑一小段距离)。质量 m 和质量 2m 应该在同一时间到达终点,当我们尝试时,我们发现它们如图 Fig.10-6 所示。
下一个问题是如果我们有两个不同的质量会发生什么。我们选择一个质量 m 和质量 2m ,并且应用我们的爆炸交互。然后会发生什么?如果,由于爆炸,m 会以速度 v 移动,那么 2m 会以怎样的速度移动?我们也许可以重复刚刚做的实验,第二个和第三个之间的间隔为零,当我们尝试时我们得到了相同的结果,也就是,受作用的质量 m 和 2m 获得了速度 -v 和 v/2 。因此 m 与 2m 之间的直接反馈给出了相同的结果,正如 m 与 m 之间的对称反馈,它遵循 m 与第三个质量 m 之间的碰撞(它们会连在一起)。更进一步,我们发现从槽轨终点折返的质量 m 和 2m ,它们的速度(几乎)完全保留,如果它们连在一起(经过碰撞)它们会停止。
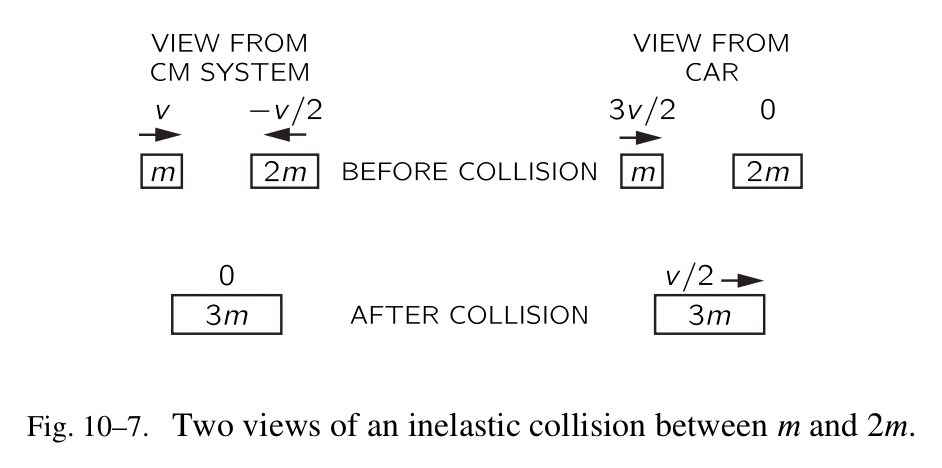
下一个问题是,如果一个带着速度 v 的质量 m 冲撞另一个静止的 2m 会发生什么。使用伽利略的相对性原理,很容易回答该问题,我们跟之前一样,从一辆以速度 -v/2 移动的汽车里观察碰撞(Fig.10-7)。(从车里看),速度是
\[v'_1=v-v(car)=v+v/2=3v/2\]和
\[v'_2=-v/2-v(car)=-v/2+v/2=0\]在碰撞之后,质量 3m 对我们来说似乎是以速度 v/2 在移动。因此我们有了答案,碰撞之前和之后的速度比是 3:1 ,如果一个质量为 m 的物体与一个质量为 2m 的静止物体相撞,那么整体会移动(连在一起),速度是 1/3 那么多。通用的规则还是质量与速度的乘积之和保持一致:mv+0 等于 3m 乘以 v/3 ,所以我们逐步地构建起动量守恒的理论。
现在我们有了一个对抗两个。使用相同的论点,我们可以预测一个对抗三个的结果、两个对抗三个,等等。两个对抗三个的示例,从静止开始,被展示在 Fig.10-8 中。
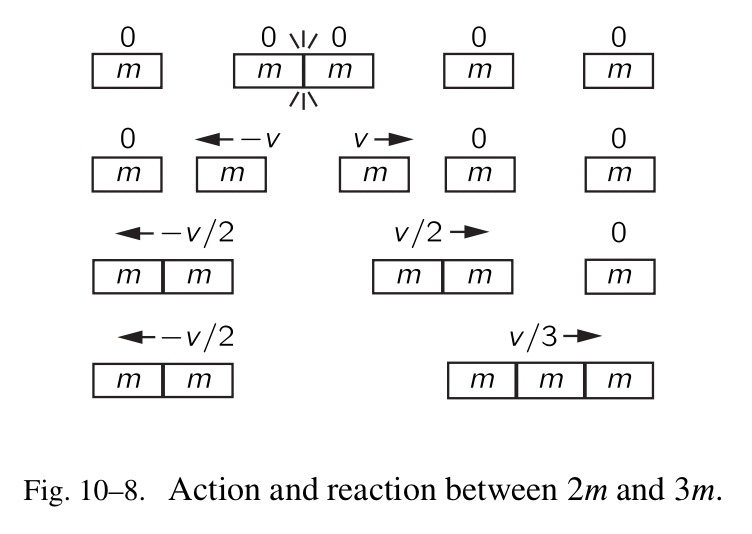
在每个示例中,我们发现第一个物体的质量乘以它的速度,加上第二个物体的质量乘以它的速度,等于最终物体的整体质量乘以它的速度。这些是动量守恒的所有的示例。从简单的、对称的示例开始,我们也通过更加复杂的示例阐述了该定律。我们实际上可以处理任意的有理的质量比率,因为每个比率非常趋近一个有理的比率,所以我们可以精确地处理每一个比率。