现在我们需要描述定律,或者规则,以各种各样的方式合并向量。第一个融合是两个向量的和:假设 $a$ 是一个向量,位于某个特定的坐标系中,它拥有三个部分 $(a_x, a_y, a_z)$ , $b$ 是另一个向量,拥有三个部分 $(b_x, b_y, b_z)$ 。现在让我们生成三个新的数字 $(a_x+b_x, a_y+b_y, a_z+b_z)$ 。它们会形成一个向量吗?我们或许会说,“它们是三个数字,任意三个数字都会形成一个向量。”不,并不是任意三个数字都会形成一个向量!为了让它成为一个向量,不仅仅需要三个数字,还需要关联一个坐标系,只有这样,在我们旋转坐标系时,这三个数字才会彼此旋转、混合,它们遵循我们之前所描述的精确的定律。所以问题变为,如果我们现在旋转坐标系, $(a_x, a_y, a_z)$ 变为 $(a_{x^{‘}}, a_{y^{‘}}, a_{z^{‘}})$ , $(b_x, b_y, b_z)$ 变为 $(b_{x^{‘}}, b_{y^{‘}}, b_{z^{‘}})$ ,那么 $(a_x+b_x, a_y+b_y, a_z+b_z)$ 会变成什么?它们会变成 $(a_{x^{‘}}+b_{x^{‘}}, a_{y^{‘}}+b_{y^{‘}}, a_{z^{‘}}+b_{z^{‘}})$ 吗?答案当然是,Yes!因为 Eq.11.5 的原型转换构成了一个线性转换。如果我们把那些转换应用到 $a_x$ 和 $b_x$ ,得到 $a_{x^{‘}}+b_{x^{‘}}$ ,我们发现转换过后的 $a_x+b_x$ 与 $a_{x^{‘}}+b_{x^{‘}}$ 相同。当 $a$ 和 $b$ 相加在一起,它们会形成一个向量,我们称之为 c 。我们写作:
\[c=a+b\]c 拥有如下特性:
\[c=b+a\]因此,我们可以写出:
\[a+(b+c)=(a+b)+c\]我们可以以任意顺序添加向量。
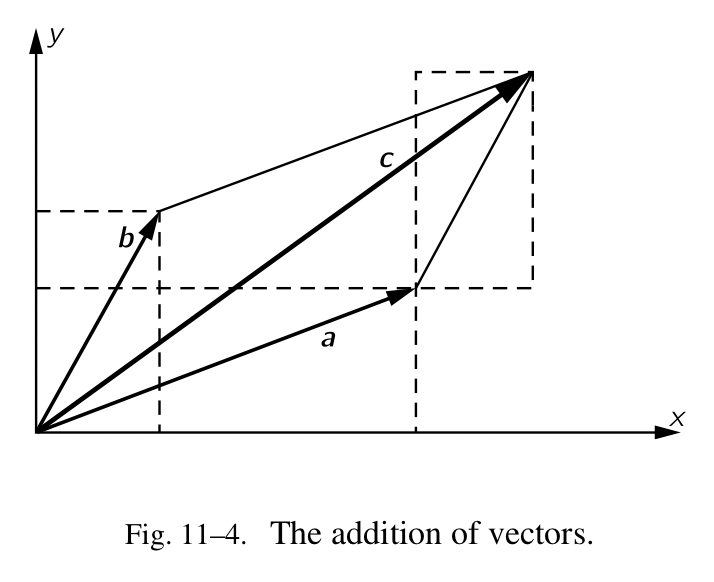
$a+b$ 的几何含义是什么?如果 $a$ 和 $b$ 由一页纸上的线段表示, $c$ 看起来会是什么样的?如图 Fig.11-4 所示。我们可以极为方便地把 $b$ 的部分添加到 $a$ 的部分,如果我们把表示 $b$ 的部分的矩形放置在表示 $a$ 的部分的矩形的旁边。因为 $b$ 正好契合它的矩形,就像 $a$ 那样,所以这跟我们把 $b$ 的“尾部”放在 $a$ 的“头部”是一模一样的,由 $a$ 的“尾部”指向 $b$ 的“头部”形成了向量 $c$ 。如果我们添加 $a$ 到 $b$ ,我们可以把 $a$ 的“尾部”放到 $b$ 的“头部”,由于平行四边形的几何特性,我们会得到相同的结果 $c$ 。请注意,向量可以使用这种方式相加,无须参照任何坐标轴。
假设我们用一个数字 $\alpha$ 乘以一个向量,这意味着什么?我们把它定义为一个新的向量,它的部分是 $\alpha a_x, \alpha a_y, \alpha a_z$ 。我们把这个问题留给学生,证明它是一个向量。
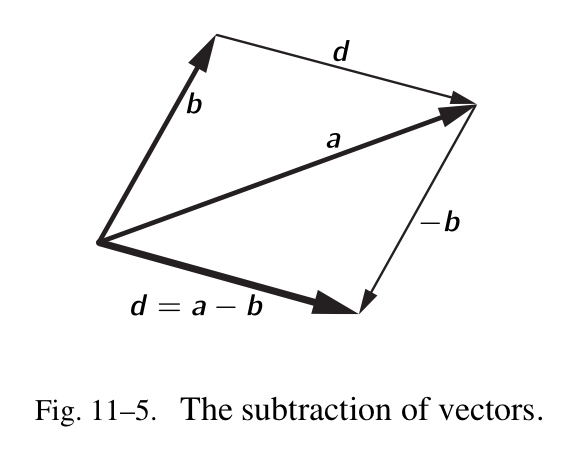
现在让我们考虑向量减法。我们或许可以像加法那样定义减法,不是相加,而是减去部分。或许我们可以通过定义一个负的向量, $-b=-1b$ ,来定义减法,然后把这些部分相加。它们是一样的。结果如图 Fig.11-5 所示。它表明 $d=a-b=a+(-b)$ 。我们也注意到 $a-b$ 的差值可以很容易地被找到,通过运用相等的关系式 $a=b+d$ 。因此差值甚至要比求和更容易找到,我们只需从 $b$ 划到 $a$ ,就能得到 $a-b$ !
接下来我们讨论速度。速度为什么是一个向量?如果位置由三个坐标 $(x, y, z)$ 给出,那速度呢?速度由 $dx/dt, dy/dt, dz/dt$ 给出。它是一个向量吗?我们可以通过求导表达式 Eq.11.5,从而搞明白 $dx^{‘}/dt$ 是否会以正确的方式转换。我们看到部分 $dx/dt$ 和 $dy/dt$ 确实依照与 x 和 y 相同的定律转换了,因此时间导数是一个向量。所以速度是一个向量。我们可以把速度写作:
\[v=d\boldsymbol{r}/dt\]速度是什么,为什么它是一个向量,也可以更加图形化地被理解:一个粒子在一个很短的时间 $\Delta{t}$ 中移动了多远?答案是: $\Delta{r}$ ,所以如果一个粒子在一个瞬间在“这儿”,在另一个瞬间在“那儿”,然后位置的向量差 $\Delta{r}=r_2-r_1$ ,它沿着如图 Fig.11-6 所示的运动方向,除以时间间隔 $\Delta{t}=t_2-t_1$ ,是“平均速度”向量。
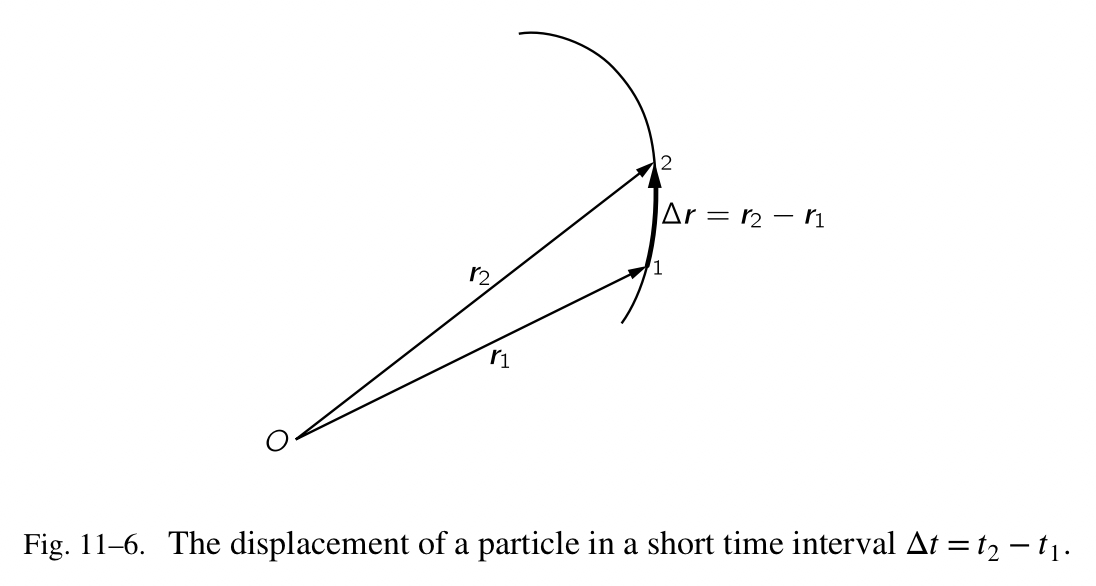
我们可以通过极限,伴随着 $\Delta{t}$ 趋近于零,在时间 $t+\Delta{t}$ 和时间 $t$ 上的半径向量的差,除以 $\Delta{t}$ , 表示向量速度。
\[v=\lim_{\Delta{t} \to 0}(\Delta{\boldsymbol{r}}/\Delta{t})=d\boldsymbol{r}/dt\]因此速度是一个向量,因为它是两个向量的差。它也是速度的正确定义,因为它的部分是 $dx/dt$ 、 $dy/dt$ 以及 $dz/dt$ 。实际上,从该论述中我们看到,如果我们求导相对时间的任意向量,我们就能生成一个新的向量。所以我们有几种生成新的向量的方法:(1)乘以一个常数;(2)相对时间求导;(3)相加或相减两个向量。