这里有另一个有趣的问题，包含概率的知识——随机游走。与抛掷硬币相似，每次游走仅仅会出现两种可能的结果，要么是向前走（假设起始位置为 x，该次距离的变化为 toward + x），要么是向后走（toward - x）。这类通用的问题涉及到气体中的原子运动——布朗运动以及测量中的误差融合。

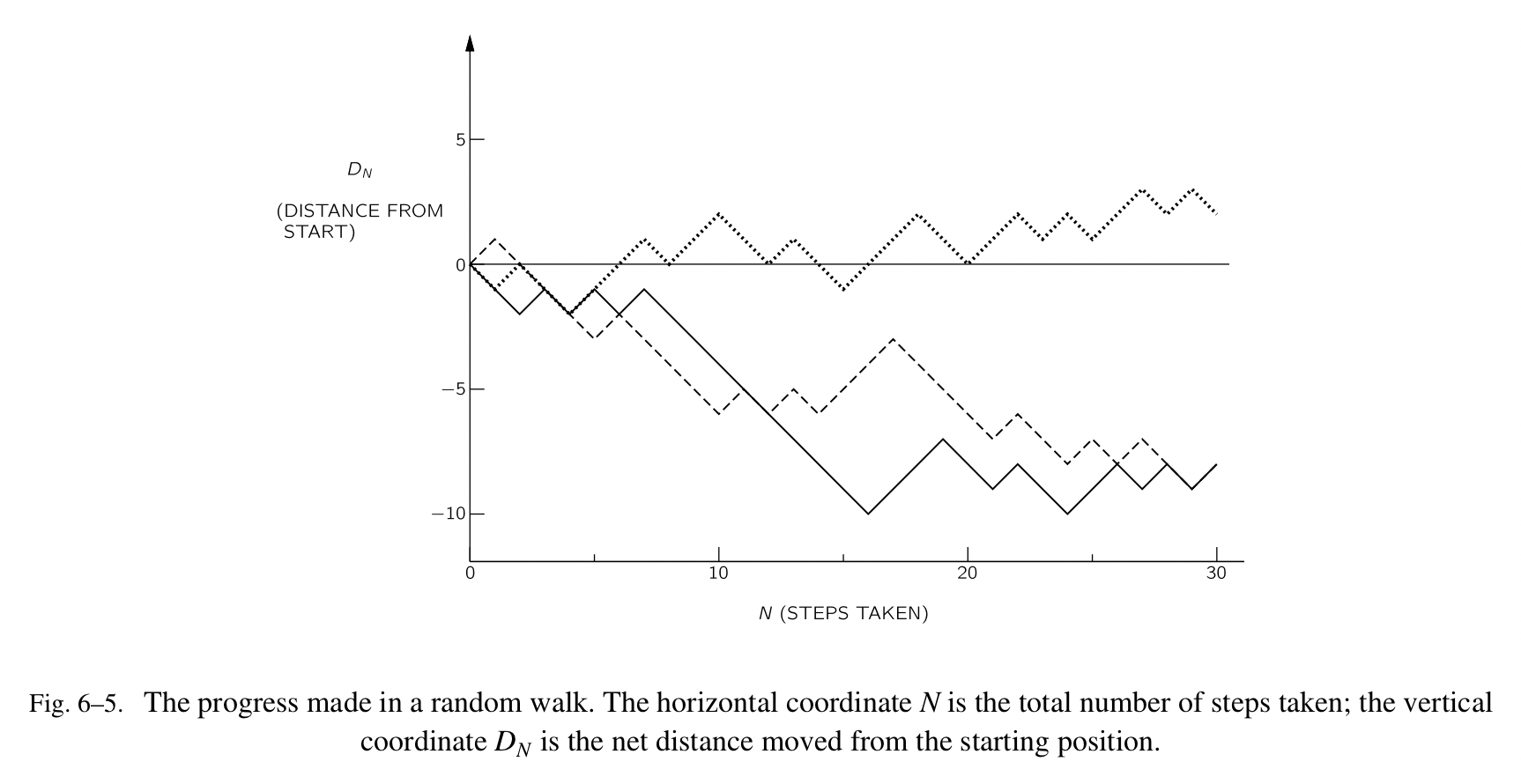
• 水平轴 N 表示整体步数；
• 垂直轴 $D_N$ 表示距离起始位置的净距离；
• 图中三条线（两条虚线和一条实线）表示三种可能游走的路径；

对于这样的运动我们会有什么疑问？也许，我们会首先问，他平均会走多远？我们一定会预期他的平均的进程是 0，因为他要么会向前走，要么会向后走，两种结果出现的可能性是相等的。但是，我们会感觉随着 N 的增加，他偏离初始位置的距离会更远。所以，也许我们会问他的平均游走距离的绝对值是多少？对于这个问题，我们可以采用另一种测量方法——距离的平方， $D^2$，处理起来会更方便。

我们可以展示 $D_N^2$ 的预期值为 N ——总步数。这里的“预期值”，也就是我们的最佳猜测，可以把它作为在许多重复进程中的预期的平均行为。我们使用 $\langle{D_N^2}\rangle{}$ 表示该值，也可把其当作均方。在第一步之后， $D^2$ 总是会 $+ 1$ ，所以我们可以表示为 $\langle{D_1^2}\rangle{} = 1$ ，这是每一步的距离单位。

对于 $N > 1$ ， $D_N^2$ 可以从 $D_{N - 1}$ 获得。如果在 $N - 1$ 步之后，我们有 $D_{N - 1}$ ，然后在 N 步之后，我们有 $D_N = D_{N - 1} + 1$ or $D_N = D_{N - 1} - 1$ ，平方之后得到：

\[D_N^2 = \begin{cases} D_{N - 1}^2 + 2D_{N - 1} + 1, \\ or \\ D_{N - 1}^2 - 2D_{N - 1} + 1, \end{cases}\]

我们的平均预期正好是上述两种可能值的平均数。 $D_N^2$ 的预期值是 $D_N^2 = D_{N - 1}^2 + 1$ ，通常情况下，对于 $D_{N - 1}^2$ ，我们应该预期其值为 $\langle{D_{N - 1}^2}\rangle{}$ ，所以：

\[\langle{D_N^2}\rangle{} = \langle{D_{N - 1}^2}\rangle{} + 1\]

因为 $D_1^2 = 1$ ，所以： \(\langle{D_N^2}\rangle{} = N\)

如果我们选择不用平方表示，可以使用均方根： \(D_{rms} = \sqrt{\langle{D^2}\rangle{}} = \sqrt{N}\)

我们已经指出随机游走与抛掷硬币非常相似，可以把游走的每一步的方向类比于抛掷硬币后出现的正面或反面，那么 D 就是 $N_H - N_T$ ——出现正面的次数与反面次数的差。因为总步数 N 为 $N_H + N_T$，两者相加之后，我们得到 $D = 2N_H - N$ 。我们之前已经推导出了关于 $N_H$ （也被称之为 k） 的表达式 $P(k,n) = \frac{(^n_k)}{2^n}$ 。因为 N 是一个常数，我们可以得到对应的 D 的分布。

从预期的值 $N/2$ 处， $N_H$ 的变化为： \(N_H - \frac{N}{2} = \frac{D}{2}\)

均方根误差为： \((N_H - \frac{N}{2})_{rms} = \frac{1}{2}\sqrt{N}\)

我们现在可以考虑一个迄今为止我们一直在规避的问题，我们怎么知道一个硬币是否“公平”？我们至少可以给出一部分的答案。对于“诚实”的硬币，我们预期其出现正面的次数的占比为 0.5，也就是： \(\frac{\langle{N_H}\rangle{}}{N} = 0.5\)

我们也预期真实的 $N_H$ 较 $\frac{N}{2}$ 偏差大约为 $\frac{1}{2}\sqrt{N}$ ，或者离差的占比为： \(\frac{1}{N}\frac{\sqrt{N}}{2} = \frac{1}{2\sqrt{N}}\)

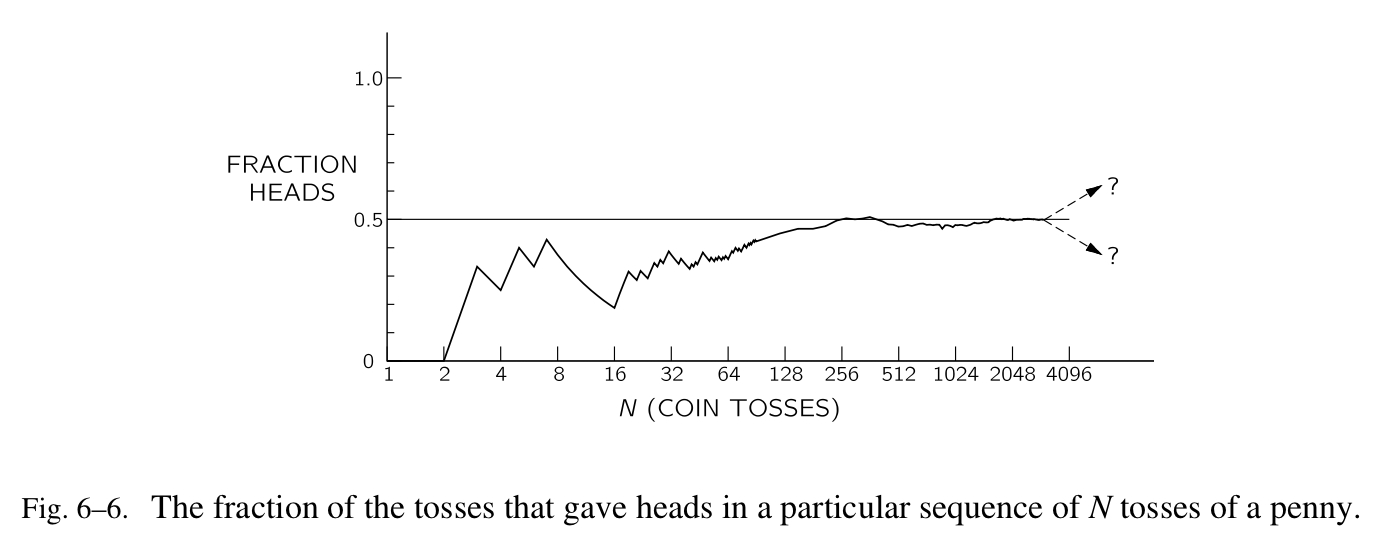
从图中我们可以看到 N 越大越接近我们的预期—— $\frac{N_H}{N}$ 为 $\frac{1}{2}$ 。但是我们也看到观察到的离差无法契合我们预期的离差，我们只能说如果离差接近 $1/2\sqrt{N}$ （within a factor of 2 or 3），我们没有理由怀疑硬币的“诚实性”，如果结果偏差很大，我可以认为硬币是“不公平的”，但是我们无法证明。

我们同样也没有考虑过像抛掷硬币这种仅仅可能存在两种结果的事物，为什么我们会愿意相信出现正面的概率与出现反面的不一样？我们定义了 $P(H) = \frac{\langle{N_H}\rangle{}}{N}$ ，对于 $N_H$ 来说，我们如何知道预期的是什么？在一些情况里，我们能够做到最好的就是在很多次抛掷中观察硬币正面出现的次数。我们必须要设置 $\langle{N_H}\rangle{} = N_H(observed)$ ，我们必须要理解不同的实验，不同的观察者，可能会导致结果 $P(H)$ 不一样。但是，我们预期的各种结果应该位于偏差 $1/2\sqrt{N}$ 之内（如果 $N_H$ 接近 $1/2$）。实验物理学家会经常说，一个由“实验定义”的概率数值会存在一定的误差，公式为： \(P(H) = \frac{N_H}{N}\pm\frac{1}{2\sqrt{N}}\)

这里有一条暗示——如果我们知道的足够多就可以计算出“真实”或“正确”的概率数值，以及观察由于数值的变化可能会存在“误差”。然而，我们没有办法可以保证这样的思考在逻辑上的一致性。也许，对于概率理论更好的理解是把它放在主观认知的层面，它总是会基于不确定的知识，而且它的数值型预期会随着我们了解的信息增多而发生改变。