为了检验缩小理论是否与其他实验中的事实相符,我们的结果证明一切都是正确的,时间也被修正,表示为方程组 15.3 的第四个等式。那是因为时间 $t_3$ ,计算的是从 B 到 C 再返回所花的,它由一个在移动的太空船里做实验的人计算所得,与另一个静止不动、正在观测该太空船的人所计算出来的不一样。对于船内的人,时间是 $2L/c$ ,但是对于另一个观测者,它是 $(2L/c)\sqrt{1-u^2/c^2}$ (Eq.15.5)。对于外部的人,他注视着船内的人正在点燃一根雪茄,所有的动作似乎都要比往常更加缓慢,但是对于内部的人,一切照旧。所以不仅仅是长度变短了,而且测量时间的设备(“时钟”)似乎也慢了下来。也就是,当船内的时钟记录时间流逝了 1 秒,正如船内的人所看到的,但是对于外面的人来说,时间流逝了 $1/\sqrt{1-u^2/c^2}$ 。
在一个移动的系统里,时钟的减缓是一个非常奇怪的现象,值得解释一番。为了理解它,我们需要查看时钟的构造,看看它在移动时,发生了什么。因为这太过于复杂,我们会使用一个简单的时钟。我们选择的时钟相当的简陋,但是在理论上,它是可以工作的:一根长杆(量尺),两端各放置一块镜子,当我们释放一个光信号,光束会不断地上上下下,在它每次下来时计作一次,有点像一个滴答作响的时钟。我们构造两个这样的时钟,它们的长度完全相等,从一开始就同步它们,在之后它们会保持一致,因为它们在长度上相同,光总是以速率 c 运动。我们把其中一个时钟交给一个人,他把它带上宇宙飞船,并把它放置在垂直于飞船运动方向的位置上;杆子的长度将不会改变。我们怎么知道垂直长度不会改变呢?他可以在每一个 y-方向的量尺上做标记,随着它们在各自的坐标系运动。两者对称,两个标记肯定是在相同的 $y-$ 和 $y’-$ 坐标处,因为不然的话,当我们把它们拿在一起比较,看到一个在上,或在下,就能知道谁在移动。
fig-15-3
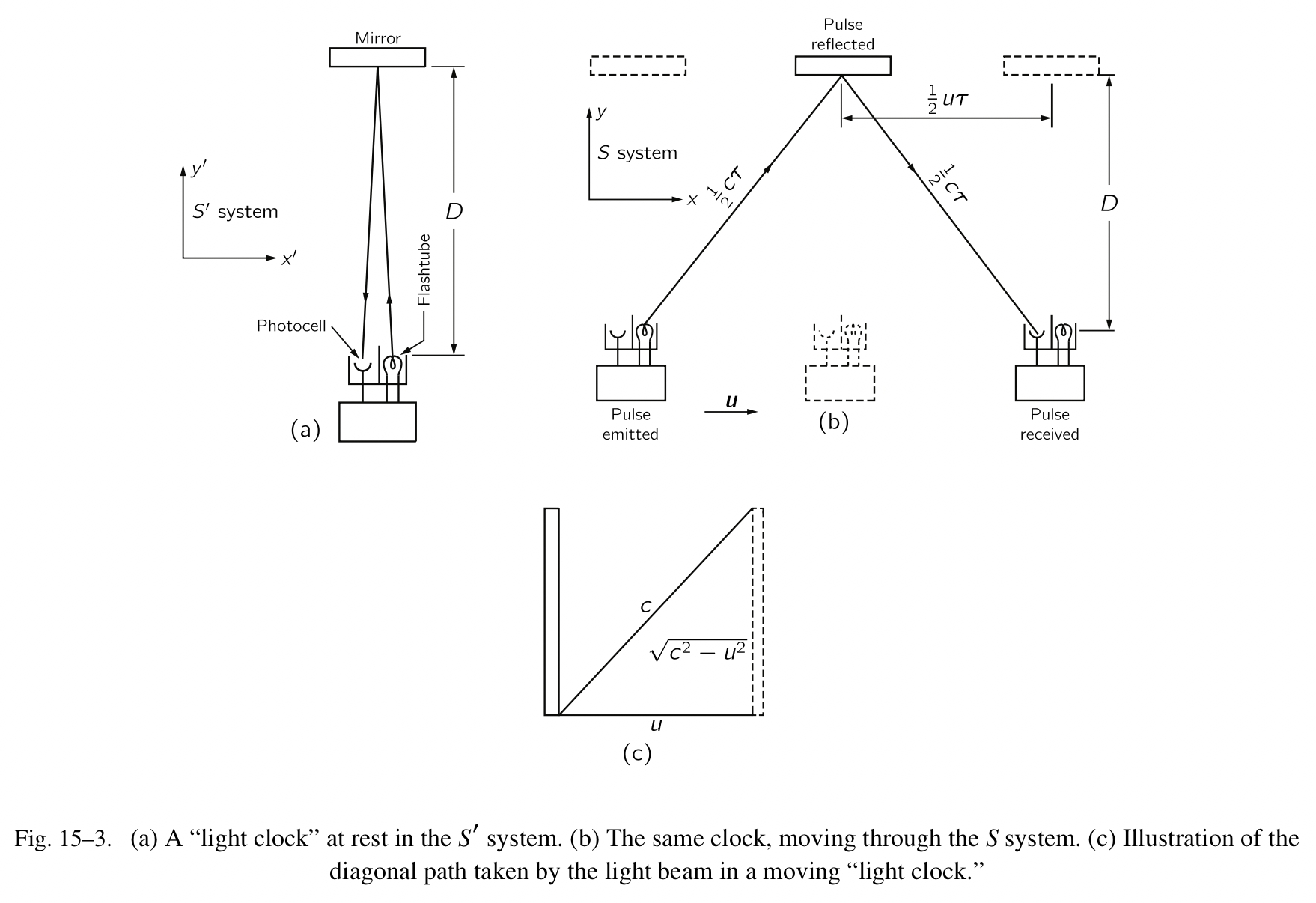
现在我们看看移动的时钟发生了什么。在他把它带上船之前,他认为它是一个精妙的、标准的时钟,当他伴随飞船运动,他不会察觉到任何异常。如果他察觉到,他就能意识到自己在运动——哪怕是由运动产生的一丁点儿改变,他就能说他在运动。但是根据相对论,在一个匀速运动的系统中是不可能的,所以什么都不会改变。另一方面,当外部的观测者注视着移动的时钟,他看到光,从一个镜子到另一个镜子,它“真的”是一个锯齿形的路径,因为杆子一直在向旁边运动。我们在迈克耳孙-莫雷实验中分析过这种锯齿形运动。如果在一个给定的时间内,杆子向前移动一段距离,该距离与 Fig.15-3 中的 u 成正比,在相同的时间内,光线移动的距离与 c 成正比,垂直的距离因此与 $\sqrt{c^2-u^2}$ 成正比。
光在移动的时钟内从一端到另一端所花费的时间要比在静止的时钟内所花费的要长。因此两次“滴答”之间的间隔,对于移动的时钟来说,更长,该间隔与三角形的斜边成正比(该斜边是我们等式中的平方根表达式的源头)。从图示中也可以看出,u 越大,移动的时钟运行的就越发缓慢。不仅仅这样的时钟会变慢,如果相对论没错,其他的时钟,无论它做任何的操作,都会变得更慢,我们不需要作进一步分析就能这样讲。为什么?
为了回答上面的问题,假设我们有两个其他的时钟,被制作地完全一样,有齿轮构成,或者基于放射性,亦或是其他的东西。然后我们调整这些时钟,让它们与我们之前的时钟保持同步。当光在之前的时钟内窜到上面再返回,我们把它的到达标记为一次,新的模式也完成了某种循环,它们由某种双次闪光,或者两次声响,亦或其他的信号,同时标记。其中的一个时钟被带到太空船上,同时还有之前的时钟。也许这个时钟不会跑得更慢,而是与静止的时钟的时间一样,这就与其他移动的时钟不同了。如果这种情况会发生,在船上的人就可以通过两个时钟的差异去确定太空船的速率,我们已经假定这是不可能的。我们不需要知道导致该效果的新时钟的内部构造是什么——我们只需要知道不管原因是啥,它会运行缓慢,就像之前的那个。
现在如果所有的时钟都跑得更慢,如果没有测量时间的方式,而只有一个更慢的比例,那么我们就可以这样讲,在一个特定的场景中,在一个太空飞船内,时间本身变得更慢了。在这里的所有现象——他的脉搏跳动、他的思考、他点燃雪茄所花费的时间以及他的生长、变老——所有的一切都以相同的比例在变慢,因为他无法说自己在移动。生物学家和医师或许会说这是不确定的,在太空船里,癌症病发的时间会更长,但是从现代物理学家的视角来看,这无疑是确定的;否则我们可以通过这个变化率确定飞船的速率!
一个非常有趣的时间变缓的例子由渺子给出,该粒子在平均生命周期 $2.2 \times 10^{-6}$ 秒之后自然地消解1。它们随着宇宙射线来到地球,也可以在实验室中被人工制造出来。它们中的一些在空中会消解,剩下的会在碰到一些物质,停止后消解。在这个短暂的生命周期内,一个渺子即使以光速运动,也不会超过 600 米。虽然渺子产生于大气层的顶部,但是它们确实可以在实验室里被发现,在宇宙射线中。这是怎么回事儿?答案是不同的渺子以不同的速率在移动,有些非常接近光速。从它们自身的视角,它们仅可存活 2 微秒,但是从我们的视角,它们可以存活相当长——足够它们中的一些抵达地球。时间增长的因子已经给出, $1/\sqrt{1-u^2/c^2}$ 。对于不同速度的渺子,它们的平均生命被测量地非常精确,该值与公式算出的几乎一样。
我们不知道介子为什么会消解,或者它的机制是什么,但是我们知道它的行为符合相对论。这是相对论的价值所在——它允许我们做出预测,即使是对那些我们知之甚少的事物。比如,在我们试图弄清楚是什么让介子消解之前,我们仍然可以预测,当它以十分之九的光速运动时,它所持续的时间为 $(2.2 \times 10^{-6})/\sqrt{1-9^2/10^2}$ 秒;我们的预测奏效了——这是一件很棒的事情。