让我们现在回到随机游走，并且考虑一个它的改版的情况。如果除了每一步的方向是随机选择的，它的步长也以某种不可预知的方式进行变化，仅有的条件是它的平均步长是一个单位。类似于这种情况，更具代表性的是气体中分子的热运动。如果我们定义步长为 S，它可以是任意的值，但是大部分情况趋近于于 1。为了特别的说明，我们应该让 $\langle{S^2}\rangle{}=1$ ，或者，等价的， $S_{rms}=1$ 。对于 $\langle{D^2}\rangle{}$ 我们的推导应该和之前一样，除了公式 6.8（ $\langle{D_N^2}\rangle{} = \langle{D_{N - 1}^2}\rangle{} + 1$ ）应该改成： \(\langle{D_N^2}\rangle{}=\langle{D_{N-1}^2}\rangle{}+\langle{S^2}\rangle{}=\langle{D_{N-1}^2}\rangle{}+1\)

我们可得到（与之前一样）： \(\langle{D_N^2}\rangle{}=N\)

对于距离 D 的分布，我们现在应该预期什么？举个例子，在30步之后， $D=0$ 的概率是多少？答案是0！概率是0说明 D 可能是任意的值，因为没有任何可能性，向后走的步长之和（步长不一样）会完全等于向前走的步长之和。我们没有办法画出像 Fig.6-2 一样的视图。

我们可以得到类似 Fig.6-2 的代表性视图，如果我们不去问得到的 D 完全等于 0，1 或者 2 的概率是多少，而是问得到的 D 接近 0，1 或者 2 的概率是多少？让我们定义 $P(x,\Delta{x})$ 作为 D 介于间隔 $\Delta{x}$ 之间，基点在 x （也就是从 x 到 $x+\Delta{x}$ ）的概率。对于 $\Delta{x}$ 我们预期 D 介于间隔之间的概率与 $\Delta{x}$ 成正比，也就是间隔的宽度。所以我们可以写出： \(P(x,\Delta{x})=p(x)\Delta{x}\)

函数 $p(x)$ 被称之为概率密度。

$p(x)$ 的形式依赖于 N ——总共执行的步数，同样也依赖于单独步长的分布。我们在这里没有办法给出证明，但是对于大数量 N， $p(x)$ 适用于所有采用单独步长的合理分布，而且仅仅依赖于 N。下图中我们画出了对应于三种 N 的值的 $p(x)$ 。

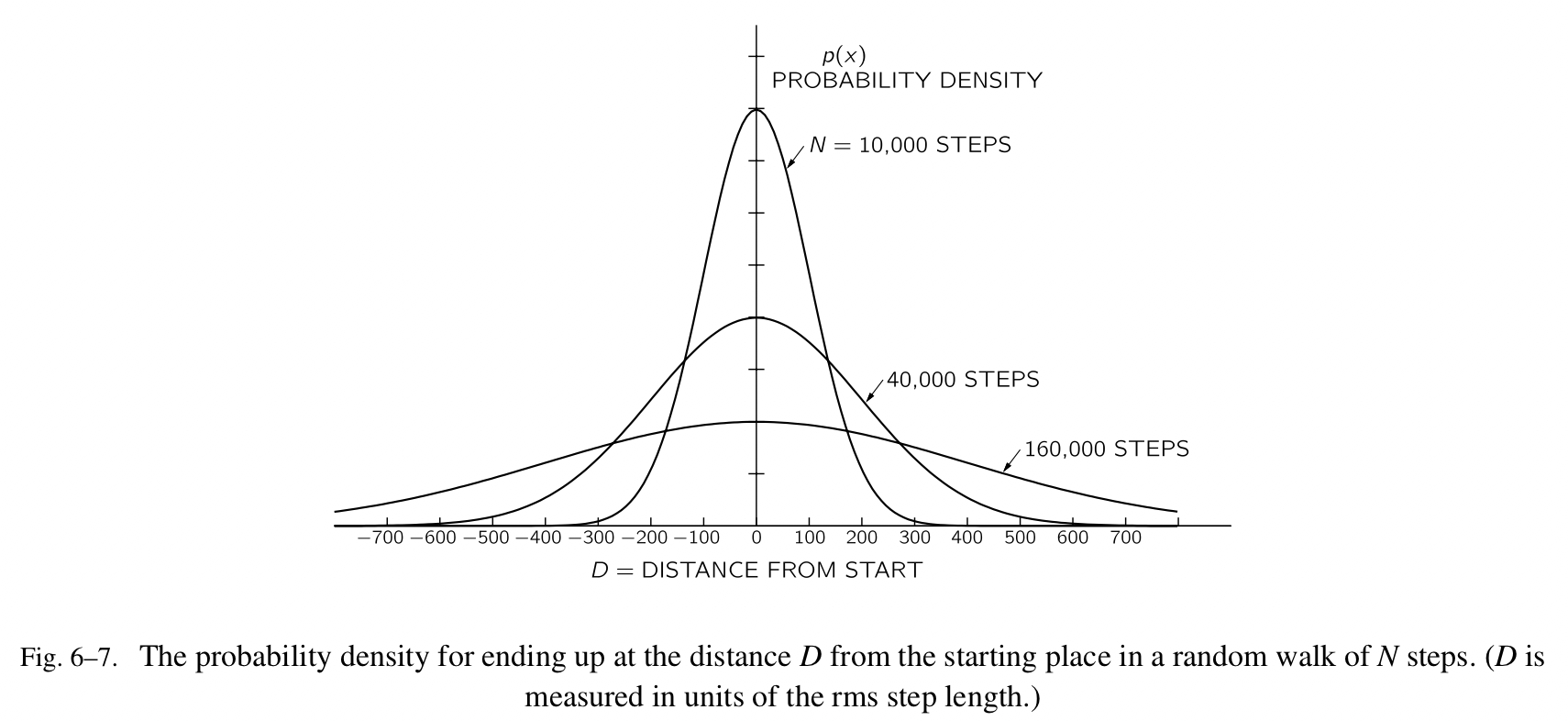
• 你将会注意到这些曲线的“半宽”（一半的宽度，通常是从 $x=0$ 开始）是 $\sqrt{N}$ ；
• 你也会注意到接近 0 的 $p(x)$ 的值与 $\sqrt{N}$ 成反比。这是因为这些曲线都是相似的形状，而且它们位于曲线下的区域必须都是相等的。因为 $p(x)\Delta{x}$ 是当 $\Delta{x}$ 很小时找到 D 介于 $\Delta{x}$ 之间的概率，我们可以定义找到 D 位于任意间隔之中（比如说从 $x_1$ 到 $x_2$）的某个地方的概率，通过把间隔拆分成很小的部分 $\Delta{x}$，并且计算出每个部分的 $p(x)\Delta{x}$ 的值，再求和。D 位于 $x_1$ 到 $x_2$ 中的某处的概率，我们也许可以写成 $P(x_1\lt{D}\lt{x_2})$，等于如下图所示的阴影区域。

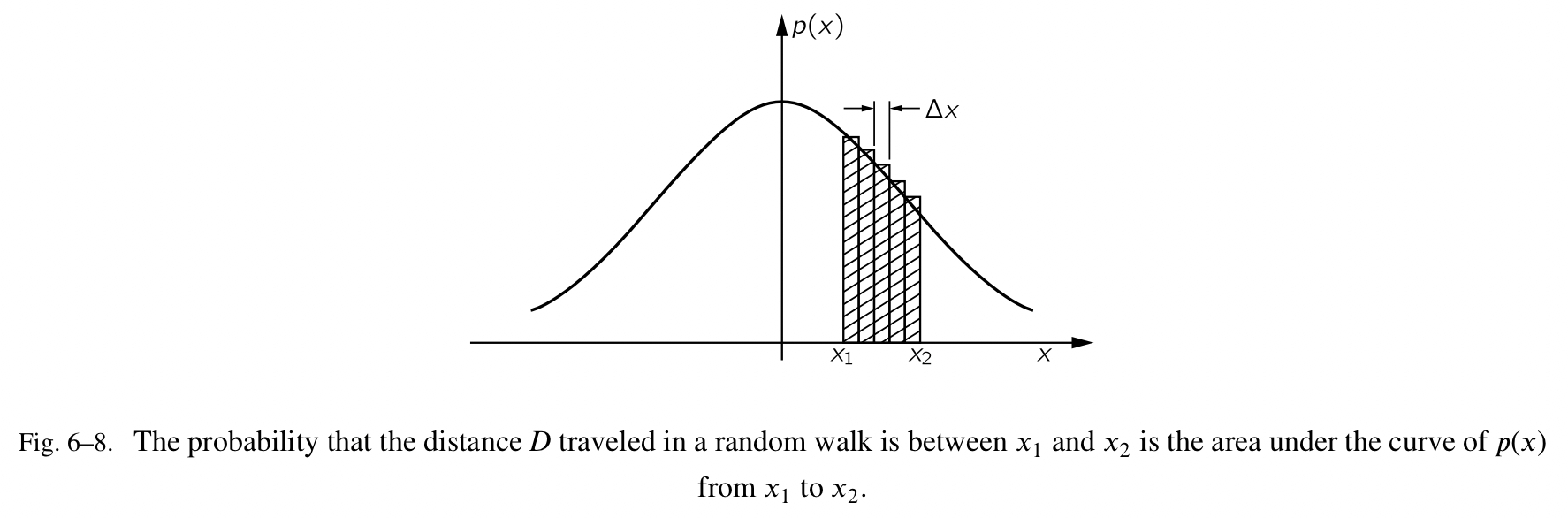
我们所拆分的 $\Delta{x}$ 越小，我们的结果就越正确。因此我们可以写成： \(P(x_1\lt{D}\lt{x_2})=\sum{p(x)\Delta{x}}=\int_{x_1}^{x_2}p(x)dx\)

位于整条曲线下方的区域是 D 位于某处的概率（也就是，某值介于 $-\infty$ 和 $+\infty$ 之间）。概率毫无疑问是 1。我们一定可以得到： \(\int_{-\infty}^{+\infty}p(x)dx=1\)

因为 Fig.6-7 曲线的宽度与 $\sqrt{N}$ 呈正比，它们的高度肯定与 $1/\sqrt{N}$ 呈正比，这样是为保证整个区域等于 1。

我们所描述的概率密度函数是遇到的最普遍的情况之一。它被称之为正态或高斯概率密度。它有数学的样式： \(p(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-x^2/2\sigma^2}\)

其中 $\sigma$ 被称为标准差，并且在我们的例子中被给出 $\sigma=\sqrt{N}$，或者，如果 $rms$ 步长不是 1，给出 $\sigma=\sqrt{N}S_{rms}$ 。

我们曾经说过在气体中一个分子的运动，或者，任意粒子的，比较像随机游走。如果我们打开了一个有机化合物的瓶子，让它的一些蒸汽进入到空气中。如果有气流，空气会旋转，气流会携带这些蒸汽。即使在完全静止的空气中，蒸汽也会扩散，直到遍及整个屋子。我们也许可以通过它的颜色或气味监测它。有机蒸气的单独分子会在静止的空气中扩散是因为它与其他的分子的碰撞导致了分子的运动。如果我们知道了平均步长和每秒执行的步数，我们可以得到其概率——一个或几个分子在任意指定的时间流逝之后，它将会被发现位于距离起点的某个地方。随着时间过去，更多的步数被执行，气体的分布会如 Fig.6-7 的连续的曲线所示。在后面的章节，我们会发现步长和步频是如何关联温度和气体压强的。

之前，我们说过气体的压强是由于分子碰撞容器壁导致的。在我们之后作更具数值化的表述时，我们希望了解到当它们碰撞时分子跑的有多快，因为它们产生的效果取决于速率。然而，我们无法谈及分子的速率。它有必要使用概率的表述。一个分子也许可以拥有任意的速率，但是某些速率相较于其他更有可能。我们描述会发生什么，是通过谈及任意指定的分子将会拥有一个介于 v 和 $v+\Delta{x}$ 之间的速率，概率是 $p(v)\Delta{v}$，其中 $p(v)$ ，一个概率密度，是速率 v 的一个给定的函数。稍后我们会看到麦克斯韦是如何通过常识和概率的观点发现 $p(v)$ 的数学表达式的。 函数 $p(v)$ 的样子如 Fig.6-9 所示。速度也许是任意的数值，但是它最可能接近最有可能的值 $p(v)$ 。

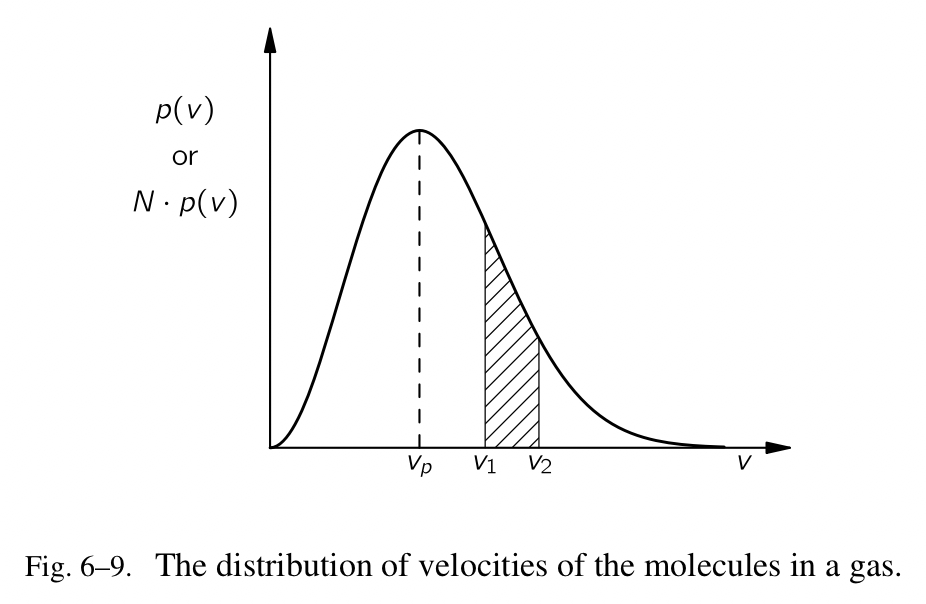
我们经常会在某种程度上以不同的方式去思考 Fig.6-9 的曲线。如果我们考虑分子是在一个典型的容器里面（它的体积是一公升），那里会有很大数量 N 的分子（ $N\approx{10^{22}}$ ）。因为 $p(v)\Delta{v}$ 指的是概率——一个分子将拥有的速度会介于 $\Delta{v}$ 之中，通过概率的定义，我们说的是预期数值 $\langle{\Delta{N}}\rangle{}$ ，被发现其速度介于间隔 $\Delta{v}$ 之中，可以被给出： \(\langle{\Delta{N}}\rangle{}=Np(v)\Delta{v}\)

我们称 $Np(v)$ 为“在速度中的分布”。位于曲线的下方速度介于 $v_1$ 和 $v_2$ 之间的区域，如 Fig.6-9 所示的阴影区域，表示（对于曲线 $Np(v)$ 来说）分子的预期的数量，其速度介于 $v_1$ 和 $v_2$ 之间。因为对于气体来说我们通常会面对很大数量的分子，我们期望较于预期数量的离差会很小（大约 $1/\sqrt{N}$ ），所以我们经常不会说“预期”数量，而会说：“分子的数量，其速度介于 $v_1$ 和 $v_2$ 之间，是曲线下方的区域。”我们应该记住，像这种陈述总是会涉及到概率数字。