接下来讨论的问题要比上面的更加复杂;它存在作用力不是常数的情况,或者不是简单地垂直的,正如我们之前的例子。我们想要一个行星,围绕太阳运动,或者,一个卫星在太空中围绕地球运动。
首先我们应该考虑一个物体从某个点 1 启动,然后坠落,朝向太阳,或者地球(Fig.13-2)。在这些情形中是否满足能量守恒定律?在这个例子中唯一的不同是,作用力随着我们的运动持续地改变,它不再是一个常数。据我们所知,作用力是 $-GM/r^2$ 乘以质量 m ,其中 m 是移动的那个质量。现在可以确定的是,当一个物体向地球坠落,动能随着下落距离的增长而增长,就像当我们不用在意作用力伴随高度改变时做的那样。问题是是否有可能找到另一个势能的公式,不同于 $mgh$ ,一个不一样的距离地球的函数,这样的话,能量守恒仍然是对的。

这个一维的情况很容易处理,因为我们知道在动能中的变化等于从运动的一端到另一端的 $-GMm/r^2$ 乘以位移 $dr$ 的积分:
eq-13-11
\[T_2-T_1=-\int_1^2GMm\frac{dr}{r^2}\]这个例子不存在余弦,因为作用力与位移都在同一个方向上。很容易计算 $dr/r^2$ 的积分;结果是 $-1/r$ ,所以等式13.11变为:
eq-13-12
\[T_2-T_1=+GMm(\frac{1}{r_2}-\frac{1}{r_1})\]因此我们有了一个有关势能的不一样的公式。等式13.12告诉我们数值( $\frac{1}{2}mv^2-GMm/r$ ),在点 1 处计算得到的,在点 2 处,或者在任意其他地方,都有一个常数值。
对于引力场中的垂直运动,我们有了势能等式。我们想到一个有趣的问题。我们能否在引力场中作出永动机?引力场会变化;在不同的位置,它沿着不同的方向,拥有不同的强度。我们可以像这样做吗,使用一个固定的,无摩擦力的轨道:起初从某点开始,把一个物体举到另外一点,然后让它绕着一个圆弧移至第三点,再把它降低一定的距离,让它进入一个特定的斜面,再把它拉出来,当我们把它带回原点,引力做了一定数量的功,物体的动能是否增加了?我们是否可以设计这个曲线,让它返回时的速度比之前的快一些,这样的话它会一直环绕下去,我们得到了永动机。因为永动机是没有可能的,我们也会发现这也是不可能的。我们会发现下面的论点:物体返回时的速度既不会更高也不会更低——它应该会在任意封闭的路径上一直环绕下去。换句话说,在引力的作用下环绕一整圈所做的功应该是零,因为如果不是零,我们会获得能量。(如果做的功被证明小于零,那么我们会获得更少的速度,当我们沿着一边运动,接下来它们会沿着另一边,因为作用力仅仅取决于位置,而不是方向,所以除非它是零,否则不管我们走哪一边,都会得到永久的运动。)
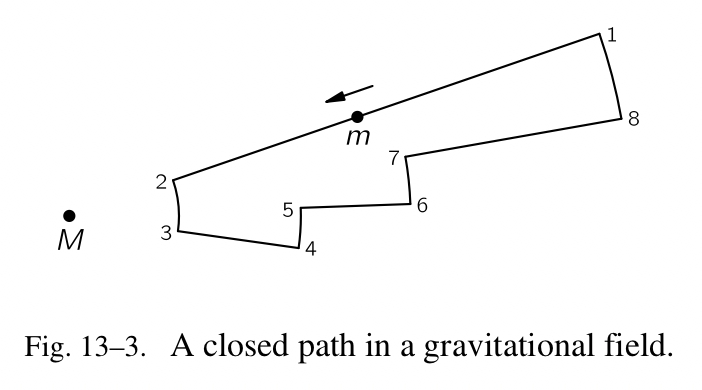
功真的是零吗?让我们论证它。首先我们会大致解释下为什么是零,然后我们会给出更棒的数学验证。假设我们使用一个简易的路径,如图 Fig.13-3 所示,一个小的质量从点 1 被带到点 2,然后绕着一个圆到达 3,回到 4,然后 5,6,7 和 8,最终又回到 1。所有的线段要么是半径,要么是圆,M 是中心。携带 m 环绕这段路径,做功多少?在点 1 和点 2 之间,是 $GMm$ 乘以这两点之间的差 $1/r$ 。
\[W_{12}=\int_1^2\boldsymbol{F}\cdot d\boldsymbol{s}=\int_1^2-GMm\frac{dr}{r^2}=GMm(\frac{1}{r_2}-\frac{1}{r_1})\]从 2 到 3,作用力完全垂直于曲线, $W_{23}=0$ 。从 3 到 4 做的功是:
\[W_{34}=\int_3^4\boldsymbol{F}\cdot d\boldsymbol{s}=GMm(\frac{1}{r_4}-\frac{1}{r_3})\]按照相同的方式,我们发现 $W_{45}=0,\quad W_{56}=GMm(1/r_6-1/r_5),\quad W_{67}=0,\quad W_{78}=GMm(1/r_8-1/r_7)$ 以及 $W_{81}=0$ 。因此
\[W=GMm(\frac{1}{r_2}-\frac{1}{r_1}+\frac{1}{r_4}-\frac{1}{r_3}+\frac{1}{r_6}-\frac{1}{r_5}+\frac{1}{r_8}-\frac{1}{r_7})\]我们注意到 $r_2=r_3$ , $r_4=r_5$ , $r_6=r_7$ 以及 $r_8=r_1$ 。因此 $W=0$ 。

或许我们会好奇这些曲线是否太少了。如果用真的会咋样?让我们尝试一下。首先,我们断言一条曲线总是可以被一系列的锯齿模拟,就像 Fig.13-4,因此,证毕,但是不加一点说明,起初并不明显,环绕一个小的三角形所做的功是零。让我们放大其中的一个,如图 Fig.13-4 所示。在三角形上从 a 到 b,再从 b 到 c 所做的功是否与直接从 a 到 c 所做的一样?假设作用力作用在一个确定的方向上,我们说三角形的边 bc 就是这个方向。我们也假设三角形非常的小,以至于作用力在整个三角形上是恒定的。从 a 到 c 所做的功是多少?
\[W_{ac}=\int_a^c\boldsymbol{F}\cdot d\boldsymbol{s}=Fs\cos{\theta},\]因为作用力是常数。现在让我们计算另外两边所做的功。在垂直的边 ab 上,作用力垂直于 $d\boldsymbol{s}$ ,因此这儿的功是零。在水平的边 bc 上,
\[W_{bc}=\int_b^c\boldsymbol{F}\cdot d\boldsymbol{s}=Fx\]因此我们看到沿着一个小的三角形的边所做的功与沿着一个斜边所做的一样,因为 $s\cos{\theta}=x$ 。我们之前已经证明过,答案是零,对于由一系列凹口组成的任意的路径,就像 Fig.13-3,如果我们走捷径,不走凹口(只要凹口足够精细,我们总是可以把凹口弄的很精细),我们所做的功也是相同的;因此在引力场中环绕任意路径所做的功是零。
这是一个令人啧啧称奇的结果。它告诉了我们之前不了解的一些事情,有关行星的运动。它告诉我们当一个行星围绕太阳运动(没有其他物体环绕,没有其他作用力),它会以这样的方式运动,在任意点上的速度的平方减去在那个点上的除以半径的某个常数总是与轨道上的每一个点相同。比如,行星离太阳越近,它的速度越快,但是快多少呢?是下面的数值:如果我们不让行星围绕太阳运动,我们改变它的速度的方向,而不是数值,让它沿着半径运动,然后让它从某个特定的半径下落至我们关注的半径,新的速率与它在真实的轨道上所拥有的一样,因为这仅仅是另一个复杂的路径的示例。只要我们返回到相同的距离,动能总是一样的。所以,不管运动是否是真实的,未干扰的,或者由于轨道,由于没有摩擦的限制,改变了方向,到达一个点的行星的动能总是相同的。
因此,我们做行星在其轨道上运行的数值分析,就像之前一样,我们可以检查是否犯了明显的错误,在计算这个常数值,每一步的能量,它不应该改变。对于表格9-2的轨道,它确实改变了,从起始到结束,大概变了 1.5% 。为什么?要么是我们在数值方法中使用了有限的间隔,要么是我们在计算中出现了一点失误。
让我们考虑在另一种情况中的能量——在弹簧上的一个质量的问题。如果我们从其平衡点处移动质量,恢复力与位移成正比。在那些情形中,我们能否找到一条能量守恒定律?当然,因为这个作用力所做的功是:
\[W=\int_0^xFdx=\int_0^x-kxdx=-\frac{1}{2}kx^2\]因此,对于在弹簧上的一个质量,其动能加上 $\frac{1}{2}kx^2$ 是一个常数。让我们看看它是如何运作的。我们把质量往下拉;它是静止的,所以其速率为零。但是 x 不是零,x 处于它的最大值,所以有某些能量,是势能。现在我们释放质量,事情发生了(细节不做讨论),在任意瞬间,动能加上势能一定是零。比如,在质量在其运动的路线上经过初始平衡点之后,位置 x 等于零,但是此刻它拥有最大的 $v^2$ ,随着它获得更多的 $x^2$ ,它会获得更少的 $v^2$ ,等等。所以 $x^2$ 和 $v^2$ 的平衡被维持,随着质量的上上下下。因此我们有了另外一条定律,弹簧的势能是 $\frac{1}{2}kx^2$ ,如果作用力是 $-kx$ 。