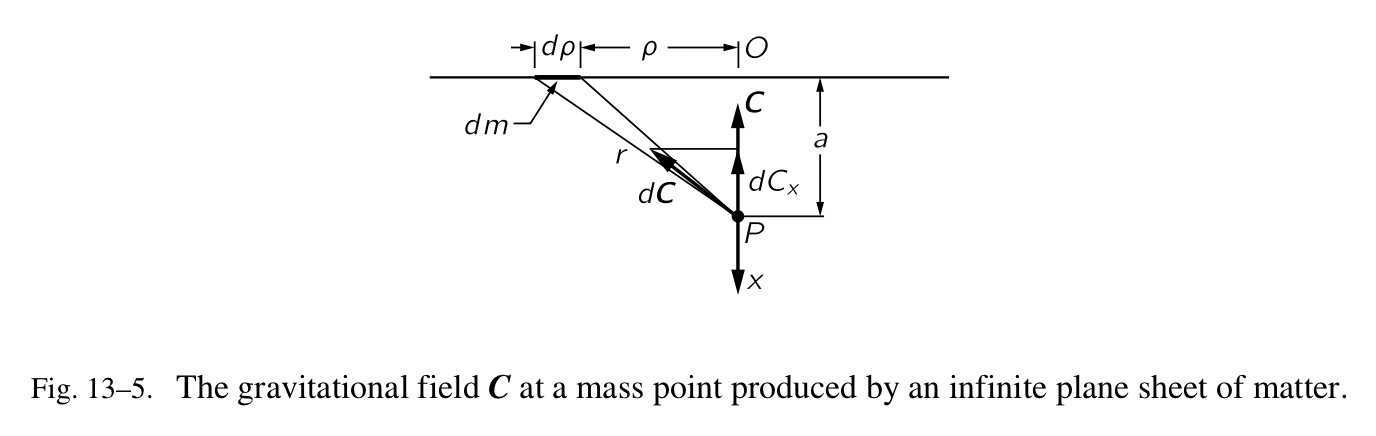
现在我们要计算场的大小，会在一些包含质量分布的物理场景中碰到。我们迄今为止还未考虑过质量分布，仅限粒子，计算这些作用力会很有趣，当它们是由不止一个粒子产生时。首先我们要求得一个质量上的引力，它是由一块平板生成，长度无限。在一个给定的 P 点处的单位质量上的作用力，由这块板子（Fig.13-5）生成，指向板子。从板子到该点的距离是 a，这个巨型板子的单位面积的质量是 $\mu$ 。我们应该假设 $\mu$ 是恒定的；它是一块均匀的板子。现在，很小的场 $d\boldsymbol{C}$ 是多少，它是由坐落于 $\rho$ 和 $d\rho$ 之间的 $dm$ 生成的，从离 P 点最近的板子上的 O 点处。答案是 $d\boldsymbol{C}=-G(dm\boldsymbol{r}/r^3)$ 。该场是沿着 $\boldsymbol{r}$ 的，我们知道仅有它的 x 部分会保留，当我们把所有小的向量 $d\boldsymbol{C}$ 相加。 $d\boldsymbol{C}$ 的 x-部分是

\[d\boldsymbol{C}_x=-G\frac{dm\boldsymbol{r}_x}{r^3}=-G\frac{dma}{r^3}\]

现在从 P 点到相同的距离 r 处的所有的质量 $dm$ 将会生成相同的 $dC_x$ ，所以我们或许会把 $dm$ 写作在介于 $\rho$ 和 $\rho+d\rho$ 之间的环中的全部质量，也就是， $dm=\mu2\pi\rho d\rho$ （ $2\pi\rho d\rho$ 是半径 $\rho$ 和宽度 $d\rho$ 的一个环的面积，如果 $d\rho \ll \rho$ ）。因此

\[dC_x=-G\mu 2\pi \rho\frac{d\rho a}{r^3}\]

因为 $r^2=\rho^2+a^2$ ， $\rho d\rho=r dr$ ，所以

eq-13-17

\[C_x=-2\pi G\mu a\int_a^{\infty}\frac{dr}{r^2}=-2\pi G\mu a(\frac{1}{a}-\frac{1}{\infty})=-2\pi G\mu\]

因此作用力与距离 a 无关！为什么？我们是否犯了错？有人或许认为我们走得越远，作用力应该越弱。并不！如果我们离近点，大部分的物质会以一个很难受的角度拉动；如果我们走远些，更多的物质会更加舒服地施加一个朝向板子的拉力。在任意距离，最有效的物质处于一个圆锥中。当我们离的越远，作用力由于反向的平方会变得越小，但是在相同的圆锥中，在相同的角度内，存在更多的物质，由于距离的平方！我们可以很细致地做这个分析，在任意给定的圆锥中，微分的贡献实际上独立于距离，因为来自一个给定质量的作用力的强度的倒数，以及被包含在圆锥中的质量大小，会随着距离的变化而变化。作用力并不是真的恒定，因为当我们到板子的另外一边，它的符号反转。

实际上，我们也解决了一个带电的问题：如果我们有一个带电的板子，单位面积的电荷是 $\sigma$ ，那么在该板子外的一个点上的电场等于 $\sigma /2\epsilon_o$ ，如果板子带正电，它的符号朝外，如果板子带负电，它朝内。为了证明，我们仅需留意，在引力中， $-G$ ，在电中，扮演相同角色的是， $1/4\pi \epsilon_0$ 。

现在我们假设有两块板子：在一个上面带有一个正电荷 $+\sigma$ ，在另一个上面带有一个负电荷 $-\sigma$ ，它与第一个相距 D 。场的大小是多少？在两块板子的外面是零。为什么？因为一个吸引，另一个排斥，作用力独立于距离，所以两个抵消了！在两块板子之间的场很明显比一块的大两倍，也就是， $E=\sigma /\epsilon_0$ ，它从正的指向负的。

现在有一个非常有趣也很重要的问题。我们一直在做假设，由地球在其表面或者在它外面的一个点上产生的作用力与地球的全部质量被放在其中心所产生的一样。这种假设的验证并不明显，因为当我们靠近时，一些质量离我们很近，另一些则很远。当我们把所有效果相加，难以置信的是最后的作用力与我们把所有的质量放在它的中间所得到的完全相同！

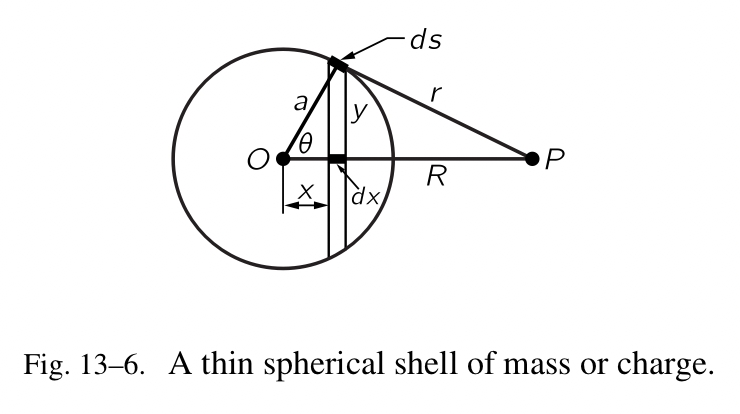
我们现在论证这个奇迹。我们需要考虑一个薄的、均匀的空心壳，而不是整个地球。壳的全部质量是 m ，让我们计算与球面中心相距距离 $R$ (Fig.13-6)的质量 $m^{‘}$ 的一个粒子的势能，证明该势能与质量 $m$ 是位于中心处所得到的一样。（势能处理起来要比场更加容易，因为我们不用担心各种角度，只需把所有质量的势能相加。）如果我们把 $x$ 称为中心点的一个平面线段的距离，那么在一片儿 $dx$ 中的所有质量与 $P$ 相距相同的距离 $r$ ，由该环导致的势能是 $-Gm^{‘}dm/r$ 。在一小片儿 $dx$ 中的质量是多少？

\[dm=2\pi y\mu ds=\frac{2\pi y\mu dx}{\sin{\theta}}=\frac{2\pi y\mu dxa}{y}=2\pi a \mu dx,\]

其中 $\mu=m/4\pi a^2$ ，是球壳上质量的表面密度。（这是一个通用的规则，球带的面积与其轴宽成正比。）因此由 $dm$ 导致的势能是

\[dW=-\frac{Gm^{'}dm}{r}=-\frac{Gm^{'}2\pi a \mu dx}{r}\]

但是我们看到

\[r^2=y^2+(R-x)^2=y^2+x^2+R^2-2Rx=a^2+R^2-2Rx\]

那么

\[2rdr=-2Rdx\]

或者

\[\frac{dx}{r}=-\frac{dr}{R}\]

因此

\[dW=\frac{Gm^{'}2\pi a \mu dr}{R}\]

所以

\[W=\frac{Gm^{'}2\pi a \mu}{R}\int_{R+a}^{R-a}dr=-\frac{Gm^{'}2\pi a \mu}{R}2a=-\frac{Gm^{'}(4\pi a^2\mu)}{R}=-\frac{Gm^{'}m}{R}\]

对于一个很薄的球壳，质量 $m^{‘}$ 的势能，在壳的外面，与壳的质量被聚集于中心所产生的一样。地球可以被想象成一系列的球壳，每一个的贡献取决于它的质量和从它的中心到粒子的距离；把它们相加，我们得到整体的质量，因此地球就相当于所有的物质都处于中心！

但是如果我们的点在壳的内部会怎样。做相同的计算，但是 P 在壳内，我们得到的仍然是两个 r 的差，但是格式是 $a-R-(a+R)=-2R$ ，或者负的与中心的距离的两倍。换言之， $W$ 变为 $W=-Gm^{‘}m/a$ ，它独立于 $R$ 和位置，也就是，在内部无论我们在哪儿，能量都相同。因此没有作用力；当我们在内部移动时，没有做功。如果势能是相同的，在内部不管一个物体被放在何处，在它上面没有作用力。所以内部没有作用力，只有外部才有，外部的作用力与质量都处于中心所产生的一样。