上面的是一系列有关对称(物理定律)的较为复杂的论述的第一个。下一个论述是我们选择什么方向的坐标轴不会有区别。换句话说,如果我们在某个地方构造了一个设备,观察它的运行,在附近我们构造了一个相同的装置,不过让它上移了一个角度,它会以相同的方式运行吗?很明显它不会,如果它是一个祖父的摆钟的话!如果摆钟保持垂直的话,它会工作,但是如果把它倾斜,钟摆会碰到内壁,什么都不会发生。这条理论在摆钟的示例中是错的,除非我们包含地球,它一直拉着钟摆。如果我们相信在旋转中物理定律对称,我们可以作出有关摆钟的预测:在时钟机械旁边,某些其他东西被包含在摆钟的操作中,我们应该在它外部寻找某些东西。我们似乎也可以预测出摆钟不会以相同的方式工作,当它被放在不同的地方(相较这个神秘的非对称源),或许是地球。我们知道摆钟在人造卫星上不会走动,因为没有有效的作用力,在火星上它会以不同的速率运行。摆钟确实包含了更多的东西,相较于内部的机械,它们包含外部的某些东西。一旦我们意识到这个因素,我们一定会让地球随着装置一起转动。当然我们无须担心;只需简单地等待一会儿,地球就会转动;然后钟摆会在新的位置上再次走动,与之前一样。当我们在旋转时,角度总是在改变;这个变化看起来并不会烦扰我们,因为我们在新的位置上所处的条件看上去与在旧的位置上的一致。这个确实困扰了一些人,因为在新的旋转位置上的定律与在未旋转位置上的相同,是对的,但是我们转动一个物体所遵守的定律与我们未转动它所遵守的相同,是错的。如果我们做非常细致的实验,我们可以说地球一直在旋转,而不是旋转了。换句话说,我们无法定位角的位置,但是我们可以说它一直在改变。
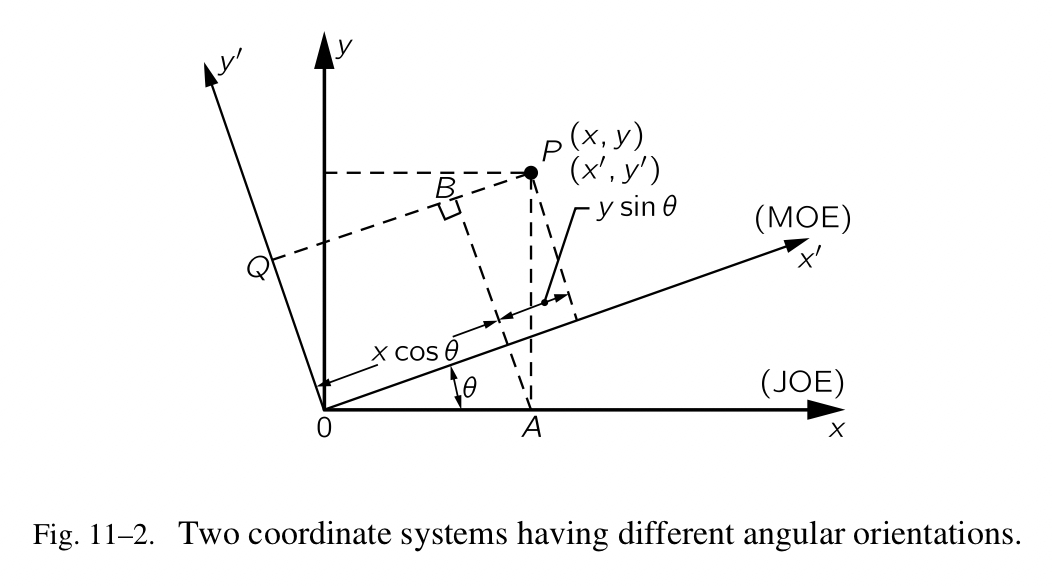
现在我们或许可以讨论物理定律中角方向的效果。让我们看看乔和莫的游戏是否会再次奏效。这一次,为了避免太复杂,我们假设乔和莫使用相同的原点(我们已经看到坐标轴可以平移到另一个地方)。假设莫的坐标轴相较乔的旋转了一个角度 $\theta$ 。两个坐标系如图 11-2 所示。任意的点 P 在乔的系统里的坐标是 $(x, y)$ ,在莫的系统里的坐标是 $(x^{‘}, y^{‘})$ 。我们应该跟上一章的例子一样,使用 $x$ 、 $y$ 和 $\theta$ 表示 $x^{‘}$ 和 $y^{‘}$ 。我们首先划出从 P 到四个坐标轴的垂直线并划出 AB 垂直于 PQ 。图形显示 $x^{‘}$ 可以写作两段长度的和,它们坐落在 $x^{‘}$ 轴上, $y^{‘}$ 写作两段长度的差,它们坐落在 AB 上。所有的这些长度都被表示为 $x$ 、 $y$ 和 $\theta$ ,参见等式 11.5,我们额外添加了一个等式。
eq-11-5
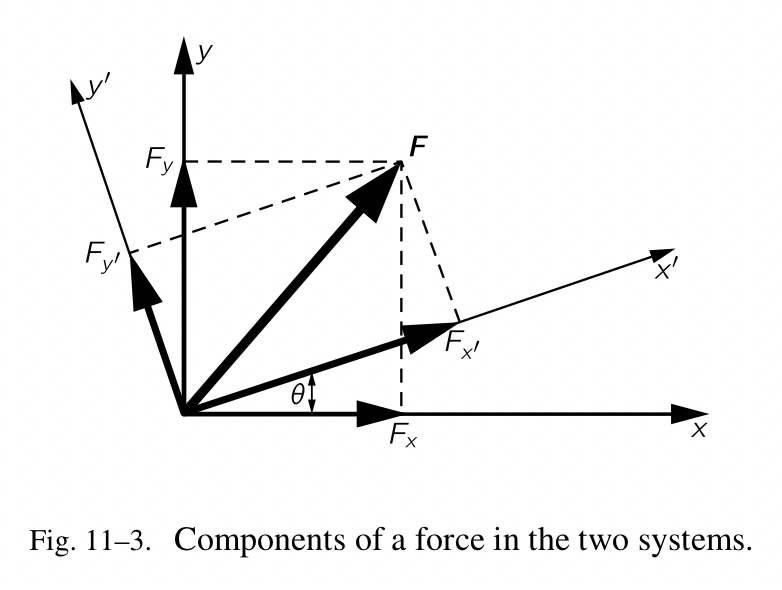
\[x^{'}=x\cos{\theta}+y\sin{\theta}\] \[y^{'}=y\cos{\theta}-x\sin{\theta}\] \[z^{'}=z\]接下来要分析由两位观察者所看到的作用力的关系,遵循跟之前一样的通用方法。让我们假设一个作用力 $F$ ,它已经被分析过,拥有 $F_x$ 部分和 $F_y$ 部分(由乔所看到的),作用在一个质量为 m 的粒子上,位于点 P,参见 Fig.11-2。为简化起见,我们移动两组坐标轴,让原点位于 P,如图 11-3 所示。莫看到 F 的部分坐落在他的坐标轴上, $F_{x^{‘}}$ 和 $F_{y^{‘}}$ 。 $F_x$ 有部分沿着 $x^{‘}$ 轴和 $y^{‘}$ 轴, $F_y$ 也有部分沿着这些轴。为了使用 $F_x$ 和 $F_y$ 表示 $F_x^{‘}$ ,我们把坐落于 $x^{‘}$ 轴上的这些部分相加,再以相似的方式使用 $F_x$ 和 $F_y$ 表示 $F_y{‘}$ 。结果是:
eq-11-6
\[F_{x^{'}}=F_x\cos{\theta}+F_y\sin{\theta}\] \[F_{y^{'}}=F_y\cos{\theta}-F_x\sin{\theta}\] \[F_{z^{'}}=F_z\]我们注意到一个意外,它非常重要,公式 11.5 和 11.6,对 P 的坐标和 F 的部分而言,它们的格式几乎完全一样。
跟之前一样,牛顿定律在乔的系统中被认为是对的,参见表达式 11.1。再问一次,莫能应用牛顿定律吗——对于他的旋转轴的系统,结果仍是正确的吗?换句话说,如果我们假设等式 11.5 和 11.6 给出了度量的关系,下面是正确的还是错误的?
eq-11-7
\[m(d^2x^{'}/dt^2)=F_{x^{'}}\] \[m(d^2y^{'}/dt^2)=F_{y^{'}}\] \[m(d^2z^{'}/dt^2)=F_{z^{'}}\]为了测试这些等式,我们可以单独地计算左边和右边,然后比较结果。让我们计算左边,我们把等式 11.5 乘以 m ,再求导两次,相对于时间,然后比较结果。这就给出:
eq-11-8
\[m(d^2x^{'}/dt^2)=m(d^2x/dt^2)\cos{\theta}+m(d^2y/dt^2)\sin{\theta}\] \[m(d^2y^{'}/dt^2)=m(d^2y/dt^2)\cos{\theta}-m(d^2x/dt^2)\sin{\theta}\] \[m(d^2z^{'}/dt^2)=m(d^2z/dt^2)\]我们计算等式 11.7 的右边,用等式 11.1 替换等式 11.6 。这就给出:
eq-11-9
\[F_{x^{'}}=m(d^2x/dt^2)\cos{\theta}+m(d^2y/dt^2)\sin{\theta}\] \[F_{y^{'}}=m(d^2y/dt^2)\cos{\theta}-m(d^2x/dt^2)\sin{\theta}\] \[F_{z^{'}}=m(d^2z/dt^2)\]快看!等式 11.8 和 11.9 的右边相等,因此我们总结如果牛顿定律在一组坐标轴上是正确的,那么它们在任意的其他坐标轴上也是有效的。对于坐标轴的平移和旋转,有确定的结果:第一,没有人可以说他的坐标轴是唯一的,但是对于特定的问题,它们会更方便。比如让引力沿着某个轴,但这不是必要的。第二,任意一个设备(它是完全地自给自足的),伴随着在装置内部完整生成作用力的所有设备,当它旋转一个角度时会工作的一样。