现在我们应该讨论涉及一些势能的观点以及有关场的观点。假设我们有两个非常大的物体 A 和 B,以及第三个非常小的,它由那两个吸引(引力),整体的作用力为 $\boldsymbol{F}$ 。我们在第 12 章已经注意到,在一个粒子上的引力可以被写作是它的质量 m 乘以另一个向量 $\boldsymbol{C}$ ,它仅仅取决于粒子的位置:
\[\boldsymbol{F}=m\boldsymbol{C}\]我们可以分析引力,通过想象,在空间中的每一个位置上都有一个确定的向量 $C$ ,它作用在我们或许会在那儿放置的一个质量上,不管我们是否在那儿放置一个质量,向量 $C$ 总是存在。 $C$ 有三个部分,每一个部分是 $(x,y,z)$ 的一个函数,空间中位置的一个函数。这样的东西,我们称为场,我们说物体 A 和 B 产生了场,也就是,它们“制造”了向量 $C$ 。当一个物体被放在一个场中,在它上面的作用力等于它的质量乘以在放置物体处的场向量的值。
我们也可以对势能做同样的事。因为势能, $(-\boldsymbol{force})\cdot (d\boldsymbol{s})$ 的积分可以被写作 $m$ 乘以 $(-\boldsymbol{field})\cdot (d\boldsymbol{s})$ 的积分,仅仅是一个标量的改变,我们看到在空间中位于一点 $(x,y,z)$ 处的一个物体的势能 $U(x,y,z)$ 可以被写作 m 乘以另一个函数,我们称其为势 $\Psi$ 。积分 $\int \boldsymbol{C}\cdot d\boldsymbol{s}=-\Psi$ ,就像 $\int \boldsymbol{F}\cdot d\boldsymbol{s}=-U$ ;在两个之间仅有一个比例因子:
eq-14-7
\[\begin{aligned} U &=-\int \boldsymbol{F}\cdot d\boldsymbol{s} \\ &=-m\int \boldsymbol{C}\cdot d\boldsymbol{s}=m\Psi \end{aligned}\]有了在空间中任意一点处的函数 $\Psi(x,y,z)$ ,我们可以立马计算出在空间中任意一点处的一个物体的势能,也就是, $U(x,y,z)=m\Psi(x,y,z)$ ——似乎微不足道。但是并非如此,因为有时用在空间中各处的 $\Psi$ 的值去描述场要比用 $\boldsymbol{C}$ 更加的方便。我们无需再写一个向量函数的三个复杂部分,可以使用这个标量函数 $\Psi$ 。更进一步,势 $\Psi$ 要比任意的 $\boldsymbol{C}$ 的部分更容易计算,当场是由一些质量生成时,因为势是一个标量,只用相加,而无需担心方向。同样地, $\boldsymbol{C}$ 可以很容易从 $\Psi$ 求得,很快就能看到。假设我们有点质量 $m_1,m_2,…$ ,在点 $1,2,…$ 处,我们想知道在某个任意点 $p$ 处的势。只需要简单地把在点 $p$ 处由一个接着另一个所携带的质量产生的势相加:
eq-14-8
\[\Psi(p)=\sum_i -\frac{Gm_i}{r_{ip}},\quad i=1,2,...\]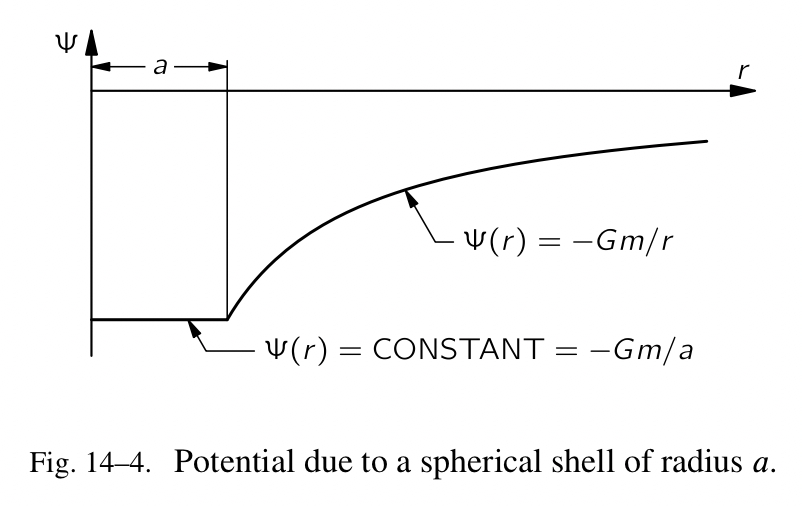
在上一章节,我们使用过这个公式,势是来自所有的不同物体的势的和,可以通过把在一个点处由壳的所有的部分所产生的势相加,求得由一个球壳所产生的势。这个计算的结果如图 14-4 所示。它是负的,在 $r=\infty$ 处为零,随着 $1/r$ 变化,向下,直到半径 $a$ ,然后在壳的内部恒定。在壳的外部,势是 $-\frac{Gm}{r}$ ,其中 m 是壳的质量,这跟把所有质量聚集于中心是一样的。但是并不是每一处都完全相同,在壳的内部势是 $-\frac{Gm}{a}$ ,它是恒定的!当势是恒定的,没有场,或者当势能是恒定的,没有作用力,因为从一个地方移动物体到另一个地方,在球的内部,由作用力所做的功是零。为什么?因为从一个地方移动物体到另一个地方所做的功等于负的势能的变化(或者,相对应的场积分是势的变化)。在内部任意两点处的势能是一样的,势能的变化为零,因此在壳的内部,在任意的两点之间移动不做功。对于所有方向上的位移,功是零,只有一种可能,那就是在那儿根本没有作用力。
这给了我们一条线索,如果给定势能,该如何得到作用力,或者场?假设我们知道在位置 $(x,y,z)$ 处的一个物体的势能,我们想知道在该物体上的作用力是多少。正如我们所见,光是知道一个点处的势无济于事,还需要知道相邻点处的势。为什么?我们是如何求得作用力的 x-部分的?(如果我们可以做到,当然,我们也可以找到 y- 和 z- 部分,然后得到整个作用力。)现在,如果我们把物体移动一个很小的距离 $\Delta{x}$ ,那么在物体上的作用力所做的功是作用力的 x-部分乘以 $\Delta{x}$ ,如果 $\Delta{x}$ 足够地小,这等价于从一点移到另一点的势能的变化:
eq-14-9
\[\Delta{W}=-\Delta{U}=F_x\Delta{x}\]对于非常短的路径,我们曾用过公式 $\int \boldsymbol{F}\cdot d\boldsymbol{s}=-\Delta{U}$ 。现在我们除以 $\Delta{x}$ ,求得作用力:
eq-14-10
\[F_x=-\Delta{U}/\Delta{x}\]当然这是不准确的。我们真正想要的是 (14.10) 的极限,随着 $\Delta{x}$ 变得越来越小,因为只有在非常小的 $\Delta{x}$ 的极限中,它才是正确的。我们意识到这是 $U$ 相对于 $x$ 的导数,我们更愿意把它写作 $-dU/dx$ 。但是 $U$ 取决于 $(x,y,z)$ ,数学家发明了一个不同的符号,来提醒我们要非常地小心,当我们在求导这样的函数时,以便于我们牢记我们只考虑 $x$ 改变, $y$ 和 $z$ 不会改变。不是 $d$ ,而是一个“反向6”,或者 $\partial$ 。( $\partial$ 应该从微积分一开始就被使用,因为我们总是想取消 $d$ ,但是我们从未想取消 $\partial$ !)所以他们写作 $\partial{U}/\partial{x}$ ,更进一步,出于强迫症,如果他们想非常地认真,会在它旁边划条线,在底部写小的 $yz$ ( $\partial{U}/\partial{xyz}$ ),这表示“ $U$ 相对于 $x$ 的导数,保持 $y$ 和 $z$ 恒定。”大多数时候,我们不会写标记,关于保持谁恒定,因为可以从上下文读出,所以我们一般不会使用 $y$ 和 $z$ 的划线。总是使用 $\partial$ ,而不是 $d$ ,作为一个警告,它是一个涉及保持某些其他变量恒定的导数。这被称之为偏导数;它是一个我们只改变 $x$ 的导数。
因此我们发现在 x-方向上的作用力是负的 $U$ 相对于 $x$ 的偏导数:
eq-14-11
\[F_x=-\partial{U}/\partial{x}\]相似地,在 y-方向上的作用力,可以通过寻求 $U$ 相对于 $y$ 的导数求得,保持 $x$ 和 $z$ 恒定,当然,第三个部分,是相对于 $z$ 的导数,保持 $y$ 和 $x$ 恒定:
eq-14-12
\[F_y=-\partial{U}/\partial{y},\quad F_z=-\partial{U}/\partial{z}\]这就是从势能得到作用力的方式。我们用完全一样的方式从势得到场:
eq-14-13
\[\begin{align*} C_x=-\partial{\Psi}/\partial{x}, \\ C_y=-\partial{\Psi}/\partial{y}, \\ C_z=-\partial{\Psi}/\partial{z}. \end{align*}\]顺带一提,我们在这儿介绍另一个符号,我们应该有很长时间没有使用它:因为 $\boldsymbol{C}$ 是向量,有 $x-,y-,z-$ 部分,生成了 $x-,y-,z-$ 部分的符号 $\partial/\partial{x},\partial/\partial{y},\partial/\partial{z}$ 有点类似向量。数学家发明了一个无与伦比的符号, $\nabla$ ,被称之为“grad”,或者“梯度”,它不是一个数值,而是一个操作符,它可以把一个标量变为一个向量。它有下面的部分,“grad”的 x-部分是 $\partial/\partial{x}$ ,y-部分是 $\partial/\partial{y}$ ,z-部分是 $\partial/\partial{z}$ ,于是我们可以这样写:
eq-14-14
\[\boldsymbol{F}=-\nabla U,\quad \boldsymbol{C}=-\nabla \Psi\]使用 $\nabla$ 可以让我们快速地测试我们是否真的有一个向量等式,但是等式 14.14 实际上与等式 14.11、14.12、14.13 完全相同;它只是书写它们的另一种方式,因为我们不想每次都写三遍等式,所以我们写作 $\nabla U$ 。
场和势的另一个示例是带电的情形。在电的例子中,在一个静止物体上的作用力是电荷乘以电场: $\boldsymbol{F}=q\boldsymbol{E}$ 。(通常,在带电问题中的作用力的 x-部分有一部分取决于磁场。从等式 12.11 中可以很容易看出,在一个粒子上由磁场产生的作用力总是与它的速度垂直,也与场垂直。因为在一个移动电荷上由磁场产生的作用力垂直于速度,在移动电荷上的磁场不做功,因为运动垂直于作用力。因此,在电场和磁场的势能的理论计算中,我们可以忽略磁场的贡献,因为它不会改变势能。)假设我们只有电场。我们可以计算能量,或者做功,与计算引力相同,计算一个数值 $\phi$ ,它是负的 $\boldsymbol{E}\cdot d\boldsymbol{s}$ 的积分,从任意固定的点到我们做计算的点,那么在一个电场中的势能就是电荷乘以这个数值 $\phi$ :
\[\begin{align*} \phi(\boldsymbol{r})=-\int \boldsymbol{E}\cdot d\boldsymbol{s}, U=q\phi \end{align*}\]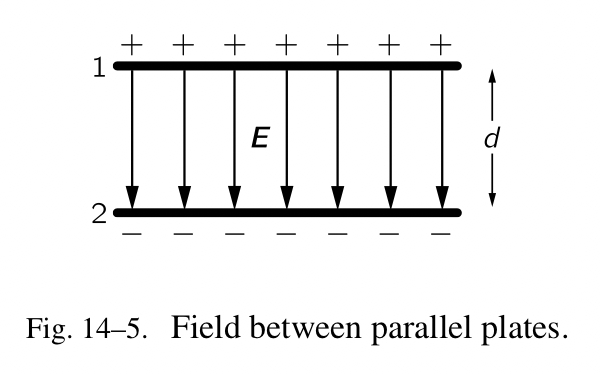
我们举一个例子,两个平行的金属片儿,每一个的表面带有 $\pm\sigma$ 电荷,每单位范围。这被称之为平行电容。在片儿的外面,作用力为零,在它们之间,有一个恒定的电场,从 $+$ 导向 $-$ ,数值为 $\sigma/\epsilon_0$ (Fig.14-5)。我们想知道从一片儿携带一个电荷到另一片儿需要做多少功。功是 $(\boldsymbol{force})\cdot d\boldsymbol{s}$ 的积分,可以被写作电荷乘以在片儿 1 处的势的值减去在片儿 2 处的:
\[W=\int_1^2 \boldsymbol{F}\cdot d\boldsymbol{s}=q(\phi_1-\phi_2)\]我们可以算出积分,因为作用力是恒定的,如果金属片儿的间隔是 $d$ ,那么积分就是:
\[\int_1^2 \boldsymbol{F}\cdot d\boldsymbol{s}=\frac{q\sigma}{\epsilon_0}\int_1^2 dx=\frac{q\sigma d}{\epsilon_0}\]势的差, $\Delta{\phi}=\sigma d/\epsilon_0$ ,被称之为电压差,单位是伏特。当我们说一对金属片儿被加上确定的电压,那么两个金属片儿的电势差是这么多伏特,是什么意思。对于一个电容,由两个平行的金属片儿构成,表面带有 $\pm \sigma$ 电荷,那么这对金属片儿的电压,或者电势差是 $\sigma d/\epsilon_0$ 。