我们应该把分析限制在力学，因为我们拥有足够的知识。在上一章节里我们看到对于每一个粒子，力学定律可以总结为三个等式：

eq-11-1

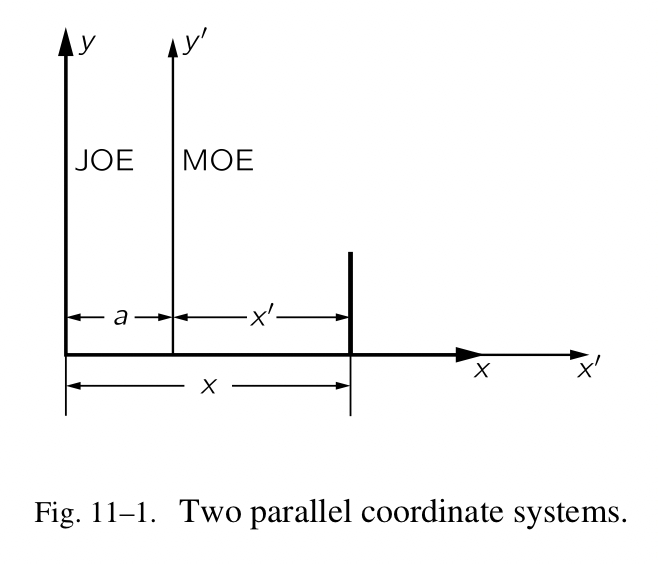
\[m(d^2x/dt^2)=F_x\] \[m(d^2y/dt^2)=F_y\] \[m(d^2z/dt^2)=F_z\]

这就意味着存在一种方法可以测量 x、y 和 z 在三个垂直轴上，作用力沿着那些方向，这样的话定律才是对的。它们必须从原点测量，但是我们该把原点放哪呢？牛顿首先会告诉我们，可以从某些地方测量，也许是宇宙的中心，这样的话定律才是对的。但是我们立马可以发现，我们是找不到中心的，因为如果我们使用某些其他的原点，并不会有什么差异。换句话说，假设有两个人，乔在一个地方有一个原点，莫有一个平行系统，它的原点在另一个地方（Fig. 11-1）。当乔在空间里测量某点的位置时，他发现它位于 x、y、z 处（我们通常会舍掉 z，因为在图中把它画出来会比较困难）。换句话说，当莫在测量相同的点时，会得到一个不同的 x（为了区分，我们称它为 $x^{‘}$ ），一个不同的 y，虽然在我们的示例中它们的数值相等。所以我们会得到

eq-11-2

\[x^{'}=x-a\] \[y^{'}=y\] \[z^{'}=z\]

为了完成我们的分析，我们必须要知道莫的作用力。作用力被认为是沿着某条线上的，在 x-方向上的作用力是整体在 x-方向上的部分，它的数值等于该作用力的大小乘以其与 x-轴夹角的余弦。现在我们可以看出莫与乔使用了完全一样的投影，因此我们得到一组等式：

eq-11-3

\[F_{x^{'}}=F_x\] \[F_{y^{'}}=F_y\] \[F_{z^{'}}=F_z\]

这些是由乔和莫所看到的数值之间的关系。

问题是，如果乔知道牛顿定律，那么如果莫尝试写出牛顿定律，它们也会是正确的吗？我们从不同的原点测量会有区别吗？换句话说，假设等式 11.1 是正确的，等式 11.2 和 11.3 给出了测量的关系，那么下面的等式是正确的吗？

eq-11-4

\[(a)\quad m(d^2x^{'}/dt^2)=F_{x^{'}}\] \[(b)\quad m(d^2y^{'}/dt^2)=F_{y^{'}}\] \[(c)\quad m(d^2z^{'}/dt^2)=F_{z^{'}}\]

为了测试这些等式，我们应该求导 $x^{‘}$ 两次。首先

\[\frac{dx^{'}}{dt}=\frac{d}{dt}(x-a)=\frac{dx}{dt}-\frac{da}{dt}\]

现在我们应该假设莫的原点相对于乔的是固定的（不是移动的）；因此 a 是一个常数， $da/dt=0$ ，我们得到

\[dx^{'}/dt=dx/dt\]

所以

\[d^2x^{'}/dt^2=d^2x/dt^2\]

因此等式 11.4a 变为

\[m(d^2x/dt^2)=F_{x^{'}}\]

（我们也假设由乔和莫测量的质量是相等的。）因此加速度乘以质量与另一个人得到的是相同的。我们已找到公式 $F_{x^{‘}}$ ，通过等式 11.1 进行替换，我们发现

\[F_{x^{'}}=F_x\]

因此莫所看到的定律是相同的，他也可以写出牛顿定律，在不同的坐标系，它们仍然是正确的。这说明定义世界原点的方法并不唯一，因为定律看起来总是一样的，无论我们从何处观察。

这条也是对的：如果在一个地方有一台机器，在它里面有特定种类的机械，那么相同的设备在另一个地方会表现地一致。为什么？因为一台机器在由莫分析时，有完全相同的等式，正如另外一台由乔分析的那样。因为等式相同，现象也会一样。所以要证明一台装置在新的位置上与其在旧的位置上表现一致，就是要证明在空间位移时等式能否再现。因此对于平移，物理定律是对称的，对称的意思是当我们平移坐标系时，定律不会改变。在直觉上很明显它是正确的，讨论与之相关的数学会蛮有趣。