之前的思考表明想要真正的理解牛顿定律需要讨论作用力，本章节的目的就是引出这种讨论，作为牛顿定律的一种补充。我们已经学习了加速度的定义和相关的理念，现在我们需要学习作用力的属性，这一章节，不像之前的，不会那么精确，因为作用力相当复杂。

让我们从一个特定的作用力开始，在空气中穿梭的飞行器上的阻力。它的定律是什么？（每一个作用力都有一个定律！）很难想象该定律是简单的。在空气中穿梭的飞机上的阻力是如何产生的——空气冲刷着机翼，在后面打转，围绕机身持续变化，还有很多其他的东西，这怎么可能是一个简单的定律呢。另一方面，让人惊奇的是飞机上的阻力近似为一个常数乘以速度的平方， $F\approx cv^2$ 。

那么这个定律是什么样的，它可以类比于 $F=ma$ 吗？绝不，因为首先这个定律是一个实验性的产物，它是经由风洞中的测试粗略所得。你说，“ $F=ma$ 或许也是实验性的。”这不是它们存在差异的原因。区别不在于实验性，而在于，就像我们理解的自然，这个定律产生于大量的、极其复杂的事件，不是一个简单的东西。如果我们学习的越来越多，测量的越来越精确，这个定律会变得更复杂，而不是简单。另一方面，随着我们越来越细致地学习飞机上的阻力定律，我们会发现它越来越“不对头”，研究的越是深入，测量的越是精确，真相越是扑朔迷离；所以我们认为它不是源于一个简单的、基础的过程，跟我们最初的猜测一致。举一个例子，如果速度非常低，一个普通的飞行器未能飞行，随着飞机在空气中缓慢穿梭，定律改变了，阻力摩擦更多地取决于线性速度。再举一个例子，作用在一个球体或气泡，亦或在黏稠如蜂蜜的液体中缓慢流动的任意物体上的摩擦阻力，与速度成正比，但是对于高速运动，流体会打转（蜂蜜不会，但是水和空气会），阻力变得几乎跟速度的平方成正比（ $F=cv^2$ ），如果速度持续增加，即使是这个定律也会失效。有人会说，“系数轻微地改变。”避开了问题。其次，还有其他复杂的东西：飞机上的作用力可以拆分吗？或者拆分为一个机翼上的作用力，前面的一个作用力，等等，去分析？实际上，是可以做到的，如果我们考虑各处的力矩，但是我们需要知道机翼上的作用力的特殊定律，以及其他的。令人吃惊的是一个翅膀上的作用力取决于另一个翅膀上的：另一方面，如果我们把飞机的部分，仅仅一个翅膀放到空气中，那么它的作用力是不相同的，如果我们把飞机剩下的都放在那儿。原因是，冲击前端的一些风流转到机翼上，改变了机翼上的作用力。这看起来是一个奇迹，竟然存在一个简单的、粗略的、实验性的定律，可以被应用到飞机的设计，但是这个定律不能归于物理的基础定律，进一步地学习只会让它越来越复杂。学习系数 $c$ 是如何取决于飞机的前端形状，让它变得微妙且令人沮丧，从来都没有一个简单的定律可以通过飞机的形状确定其系数。相对而言，引力定律是很简单的，进一步地学习只会让它更加简单。

我们刚刚讨论了摩擦力的两个示例，空气中的高速运动和蜂蜜中的缓慢流动。还有另一种摩擦力，被称为干摩擦力或滑动摩擦力，当一个固态物体在另一个上滑动时产生。这种情况，作用力需要维持运动。它被叫做摩擦阻力，它的初始，也很复杂。站在原子的级别，接触的表面都是不规整的。在接触面上的许多地方，原子看起来是一个整体，随着物体的滑动，原子被划开，产生了振动；类似的事情一定会发生。这个摩擦力的机制之前被认为是非常简单的，表面凹凸不平，摩擦力源于举起滑块越过凸起；然而并非如此，因为在该过程中没有能量损失，实际上能量是被消耗的。能量损耗的机制是，随着滑块划过凸起，凸起变形，产生了波和原子运动，以及，随后的，热量，在两个物体之中。令人惊奇的是，通过实验所得，这个摩擦力可以大致由一个简单定律阐释。这个定律是，需要克服摩擦才能在一个物体上拖拽另一个的作用力取决于在接触的两个表面之间的垂直作用力（它垂直于表面）。实际上，我们可以近似地认为，摩擦作用力与这个垂直作用力成正比，有一个常量系数；也就是：

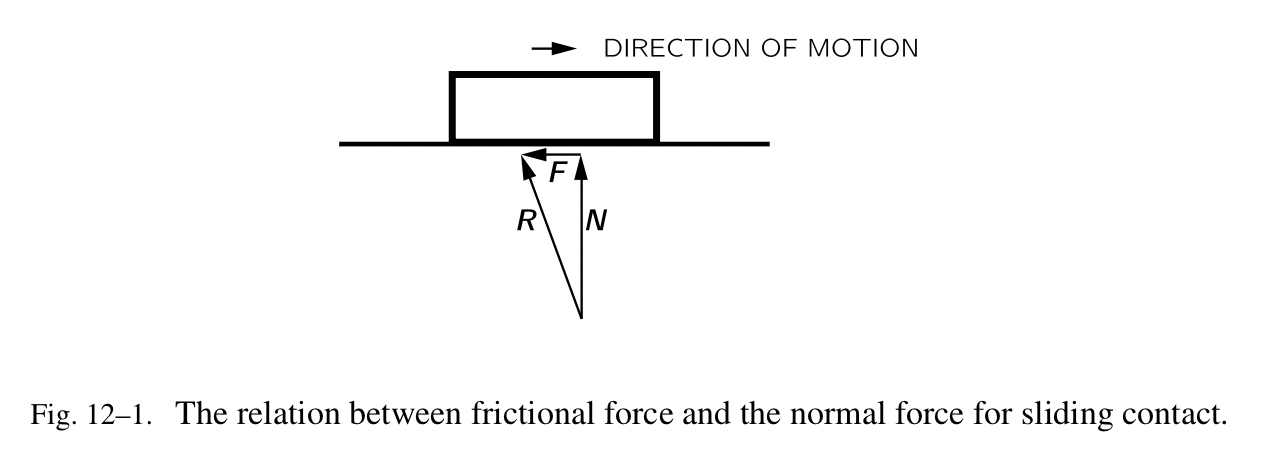
\[F=\mu N\]

其中 $\mu$ 被称之为摩擦系数（Fig.12-1）。虽然这个系数并不准确，但是这个公式是一个很棒的实验性的规则，被用于估算特定情形中的作用力的大小。如果垂直作用力或运动的速度过大，定律失效，因为产生了过多的热量。值得注意的是每一个实验性定律都有自身的限制，超过了之后就无法奏效。

近似正确的公式 $F=\mu N$ 可以由一个简单实验阐释。我们设置一个平面，倾斜一个角度 $\theta$ ，在平面上放置一块重量 $W$ 。然后我们把斜面变得更加陡峭，直到重物在自身的重量下开始滑动。沿着平面向下的重量的部分是 $W\sin{\theta}$ ，当整个物体在滑动时，它一定等于摩擦作用力 $F$ 。垂直于平面的重量的部分是 $W\cos{\theta}$ ，它是垂直作用力 $N$ 。代入这些值，公式变成， $W\sin{\theta}=\mu W\cos{\theta}$ ，我们得到 $\mu=\sin{\theta}/\cos{\theta}=\tan{\theta}$ 。如果这个定律是对的，那么一个物体会在某个确定的倾角开始滑动。如果相同的重量被加载在上面，虽然 $W$ 增加了，但是公式中所有的作用力也同比例增加， $W$ 相互抵消。如果 $\mu$ 保持不变，加载的重物会在相同的斜率再次滑动。如果角度 $\theta$ 是由载着初始重量的测试决定的，我们发现即使载着更重的物体，也大致会在相同的角度滑动。即使一个重量数倍于另外一个，它也是成立的，因此我们总结摩擦系数与重量无关。

在做实验时，惹人关注的是，当平面倾斜至大致的角度 $\theta$ ，重物没有平稳地滑行，而是以一种断断续续的方式。在一个地方它或许会停止，在另一个地方它或许会加速。这种表现说明摩擦系数仅是一个粗略的常数，它会随着平面上位置的不同发生变化。不管重物是否加载，同样异常的表现总会被观察到。这样的变化是由不同程度的平面平滑度或硬度导致的，或许还有灰尘、氧化物，或者其他物质。那些表格中所谓的 $\mu$ 的值，像是“铁块在铁片上”、“铜块在铜板上”，等等，都是错的，因为它们忽略了上面提及的要素，它们才真正的确定了 $\mu$ 。摩擦力从来都不是由“铜块在铜板上”导致的，而是由附着在上面的杂质。

在上述实验中，摩擦力基本上独立于速度。很多人确信需要克服才能让某物启动的摩擦力（静摩擦力）要大于维持它滑行所需的作用力（滑动摩擦力），但是固态金属很难显示有什么不同。这种观点或许产生于有一点燃油或润滑剂的地方，或者某物被悬挂在弹簧上，或被绑在其他的设备上。

真的很难做摩擦力的精确的量化实验，摩擦力定律还不能很好地分析，尽管在工程领域精确的分析有着巨大的价值。只要表面是标准化的，定律 $F=\mu N$ 就相当精确，但是定律为什么是这样的，还不能真正理解。为了证明系数 $\mu$ 几乎独立于速度需要一些细致的实验，因为摩擦力会显著减少，如果低位的平面振动地非常迅速。在高速中做实验时，必须要留意的是物体不会相对于另一个振动，因为在高速中显著减少的摩擦力通常是由振动导致的。不管咋说，这个摩擦力定律是另外一种部分实验性定律，它们还没有充分地理解，纵览已经完成的所有工作，让人吃惊的是有关这个现象的更多解释还未出现。当前，我们还无法估算两个物质之间的摩擦系数。

尝试通过滑动纯净的物质测算 $\mu$ ，例如在铜板上滑动铜块，将会产生欺骗性的结果，因为接触的表面不是纯的铜，而是混合了氧化物和其他杂质。如果我们使用绝对纯的铜，如果我们清洗、抛光表面，在真空中释放气体，做好能想到的一切，我们仍然无法得到 $\mu$ 。即使我们把装置置于垂直位置，滑块也不会落下——两片铜粘合在一起！对于硬质表面，系数一般小于 1，现在成了数倍！出现这种情况的原因是，当接触的原子都是相同类型时，原子无法“识别”它们在不同的部分。当有其他原子，在氧化物和润滑剂以及介于之间的更加复杂的杂质薄层中，原子可以“识别”它们在不同的部分。当我们意识到是原子之间的作用力维系着铜块作为一个整体，这下就明朗了，对于纯金属，根本无法得到摩擦系数。

同样的现象可以在一个简单的居家实验中观察到。拿出一个玻璃碟和玻璃杯，把杯子置于碟面上，再拿一圈线绳揽住杯身拉动，我们发现它很容易就滑动了，虽然不平稳，但是确实可以感受到一个摩擦系数。接下来，浸湿碟面和杯子的底部，再次拉动，它定住了，如果我们仔细查看，应该能找到一些痕迹，因为水可以把表面的油脂和其他杂质托起来，于是我们得到了玻璃对玻璃的接触，这个接触很紧密，玻璃不会分开。