当我们知道了引力，我们还能够理解其他什么？大家都知道地球是圆的。但是为什么呢？原因很简单，那是由于引力导致的。地球仅在自己是圆的情况下才能被理解，因为一切的事物都吸引着一切其他的事物，所以它会尽可能把自己聚集在一起！如果我们更进一步讨论，地球严格来说并不是一个球体，因为它一直在旋转，这就导致了离心的效果，在赤道附近会产生与引力相反的作用力。这证明了地球应该是椭圆的，而且我们能够得到这个椭圆的正确形状。我们因此可以推导出太阳、月亮还有地球都应该是近似的椭圆，仅仅使用万有引力定律。

通过引力定律，我们还能够做什么？如果我们观看木星的卫星，我们就可以了解有关它们围绕行星运动的一切。顺便说一下，曾经有一个蛮大的困难涉及到木星的卫星，它值得被提出来。罗默很认真地研究过这些卫星，他注意到有些卫星会较计划提前，有些会延后。（我们可以发现它们的计划表，通过等待很长的一段时间，然后找出卫星平均环绕所花费的时间。）当木星离地球相当近的时候，它们会提前；当木星离地球较远的时候，它们会延后。这个很难使用万有引力定律阐释——事实上，如果给不出其他的解释，这就等于宣告了这条论点的死亡。如果一条定律在它本应该奏效的地方失灵了，那它就是错的。但是造成这种差异的原因是非常简单和美妙的：需要花一点时间才能看到木星的卫星，因为光线从木星传到地球是需要时间的。当木星离地球更近的时候，时间会花的少一点；当它离地球更远的时候，时间会花的多一些。这就是为什么卫星看起来，从平均数上，有些会提前，有些会延后的原因，这取决于它们是否离地球更近或更远。这个现象说明光线不是立即传输的，并且对光线的速度做了首次估算。这是发生在 1676 年的事儿。

如果所有的行星彼此之间相互地推拉，我们说，控制着木星围绕太阳运转的力不仅仅来自太阳，也有一部分来自其他的行星，比如，土星。这个力并不是很强，因为太阳要比土星重的多，但是依然会有一些拉力，以至于木星的轨道不会是一个完美的椭圆，实际上，确实如此；不那么准确地讲的话，它是“晃晃悠悠”地围绕椭圆的轨道运动。这样的运动会有一点复杂。尝试分析木星、土星还有天王星的运动的举动是基于万有引力定律的。行星的相互作用被计算出来，看看在其运动中的细小差异和不规律能否通过这条定律得到完整地阐释。令人惊讶的是，对于木星和土星，一切正常，但是天王星就有点“奇怪”了。它的行为表现方式很怪异。它并不是沿着一个精确的椭圆运动，但那是可以理解的，因为有来自木星和土星的吸引力嘛。可是即使把这些都考虑在内，天王星仍然走的不对，这样的话引力定律就处于被颠覆的危险之中，这个可能性不应该被排除。有两个人，Adams 和勒威耶，一个来自英国，一个来自法国，他们分别提出了另外一种可能性：也许存在另外一个行星，它是黑色的、不可见的，至少人类还没有看到它。这个行星，N，它会拉着天王星。他们计算出这个行星应该出现在哪里才会产生这些观测的差异。他们发送消息给各个观测站，“先生们，把你们的望远镜指向这里，或那里，你们将能看到一个新的行星。”这通常取决于与你共事的人是谁，看看他们是否会搭理你。他们留意到勒威耶；进行了观测，然后发现行星 N 真的在哪儿！其他的观测站随后也进行了观测，他们也发现了它。

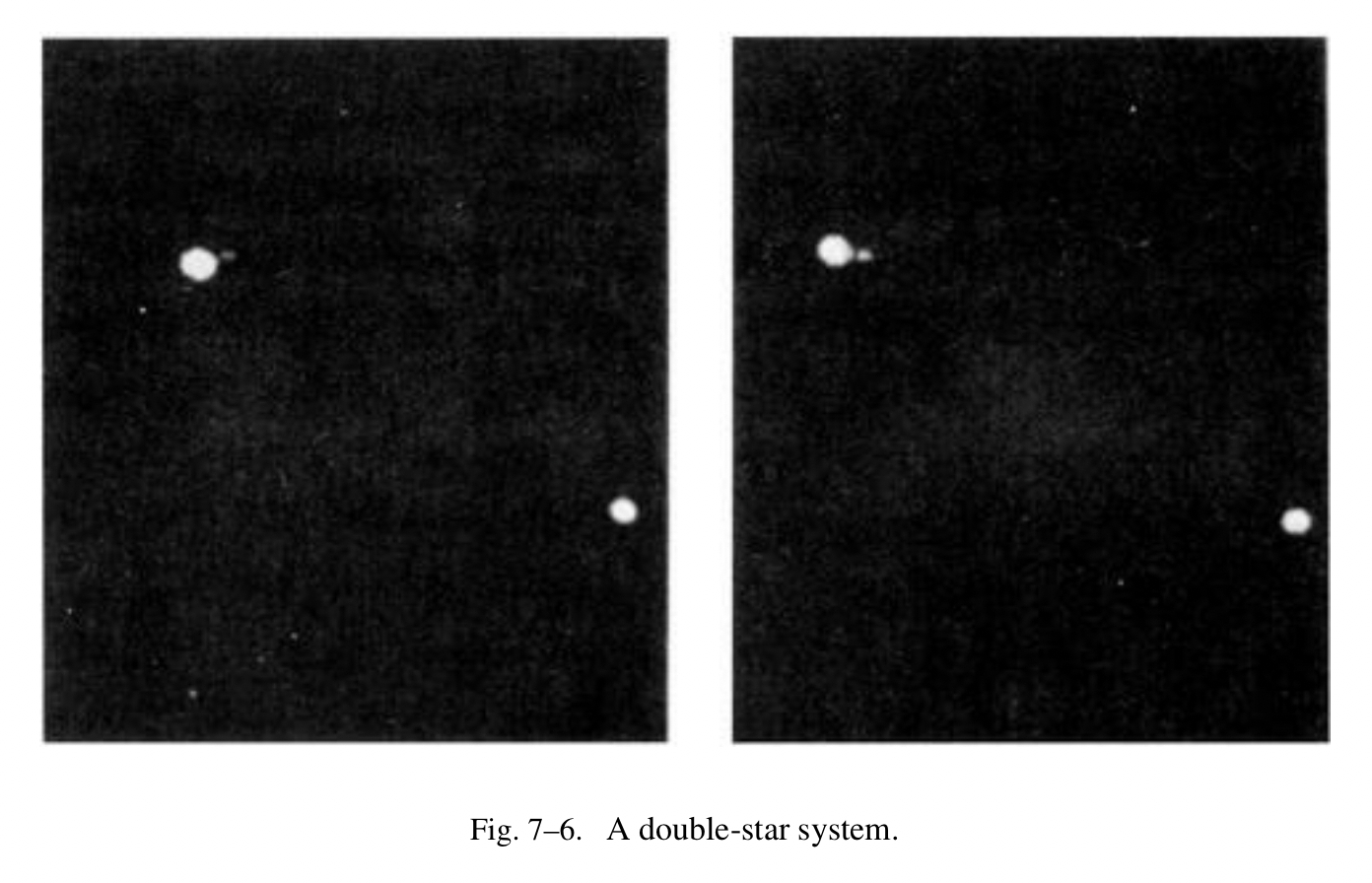
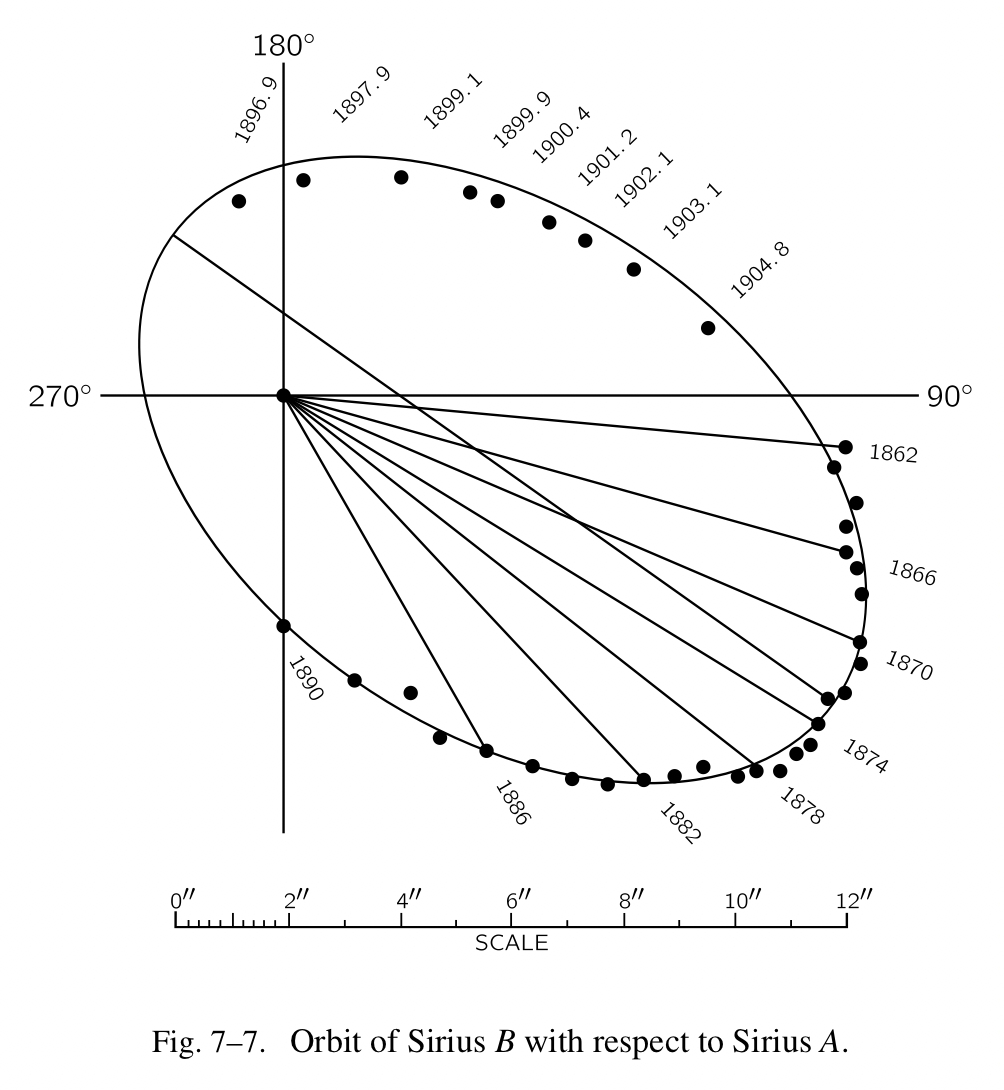
上述的发现说明牛顿的定律在太阳系中是绝对正确的；但是它们会延伸到相较最近的行星的些许距离之外吗？第一个测试蕴含在下面的问题之中，星球会跟行星一样彼此吸引吗？我们在一个双星中找到了确定的证据。Fig.7-6 显示了一个双星——两个相距非常近的星球（在图片里也应该会有第三颗星作为参照，以便于我们了解照片没有翻转）。星球也显出它们好像晚了几光年。我们看到，相对于“固定”的星球，这一对的轴在旋转，也就是说，两个星球彼此环绕。它们会按照牛顿定律旋转吗？Fig.7-7 显示出像这样的一个双星系统的相对位置的精细测量。在这里我看到了一个美丽的椭圆，从 1862 年开始测量，在 1904 年几乎转了一圈（目前为止它肯定多转了一圈）。一切都跟牛顿定律相一致，除了天狼星 A 不在焦点上。为什么会这样呢？因为椭圆平面不在“天空平面”里。我们没有采用正确的角度观测椭圆轨道，当一个椭圆以一个斜面呈现的时候，虽然它依旧是椭圆，但是其焦点不在相同的位置上。因此我们可以根据万有引力定律的要求分析双星环绕彼此的运动。

Fig.7-8 揭示了引力定律在更大的距离上依然是适用的。如果一个人看不出其中引力发挥的作用，那么他是没有灵魂的。该图例显示出天空中一个最美的事物——球状星团。所有的点都是星球。虽然它们看起来像是朝中心地带填充的实体，那是由于我们设备的缺陷导致的。实际上，在最中心的星球之间的距离是非常大的，它们几乎不会碰撞。在内部较于外部有更多的星球，随着我们向外探索，星球变得越来越少。很明显，在这些星球之中存在某种吸引。这毫无疑问说明了在很大的维度上引力是存在，也许是太阳系大小的 100,000 倍。让我们更进一步，去观察一个完整的星系，就像 Fig.7-9 所示。这个星系的形状揭示了一个明显的聚合趋势。当然我们在这里无法证明它是精确的平方反比定律，我们只能说在如此巨大的维度上依旧有某种吸引，它维持着所有的东西在一起。有人会说：“好吧，所有的一切都很清晰，但是为什么它不仅仅是一个球呢？”因为它一直在旋转，并且它拥有的角动量让它随着自身的缩小无法停止；在一个平面里它肯定会缩小很多。（顺便一提，如果你一直在寻找一个好的问题，像是螺旋臂是如何形成的，以及是什么决定了这些星系的形状的相关的精确的细节，目前还无法给出答案。）毫无疑问，星系的形状是由于引力导致的，即使我们还未能完全地分析其结构的复杂性。在一个星系里我们会有一个大概从 50,000 到 100,000 光年的区间。地球到太阳的距离是 $8\frac{1}{3}$ 光分，所以你可以看到这些维度到底有多大。

引力看起来在更大的维度上是存在的，正如 Fig.7-10 所示，它显示出许多“很小”的东西聚集在一起。这就是星系团，有点像星团。因此星系在这样的距离上彼此吸引，它们同样会聚合成团。也许引力会存在于几千万光年的距离之外；迄今为止我们知道的是，引力应该完全遵守平方反比定律。

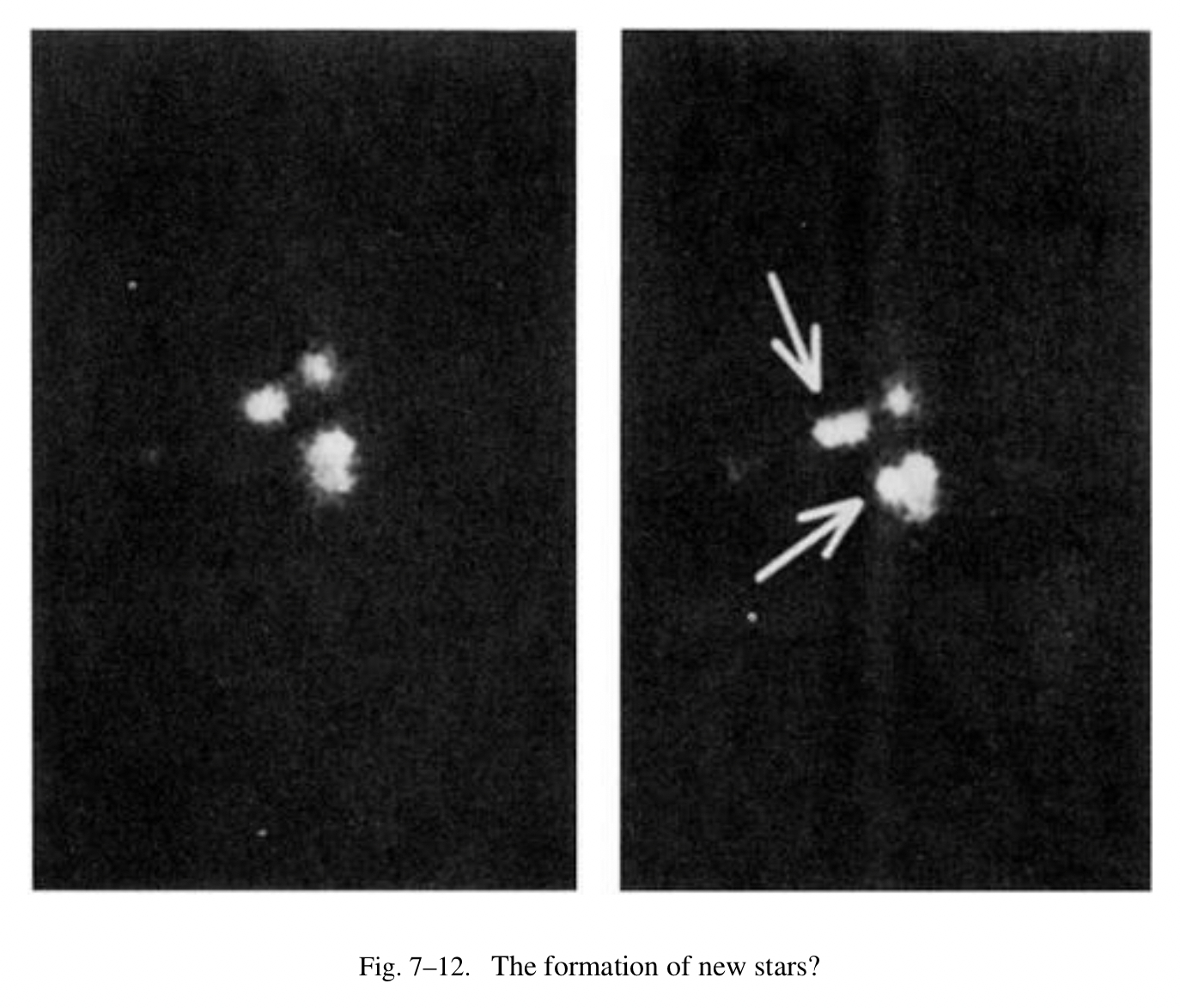
我们不仅可以理解星云，而且通过引力定律，我们可以了解到一些关于星球起源的的点子。如果我们有一个很大的由尘埃和气体组成的云团，如 Fig.7-11 所示。尘埃之间的相互吸引也许会让它们形成小的块。图例里视野所及的地方有一些“小”的黑斑，它们也许是尘埃和气体发生聚合的初始状态，在引力的作用下，形成了星球。无论我们是否看到了星球的形成仍然是有待商榷的。Fig.7-12 给出了我们能提供的一丝证据。在左边的是一个包含一些星球的近似气体的图片，它摄于 1947 年，在右边的是另一个图片，摄于 7 年之后，它显示出两个新的明亮的斑点。气体在足够强的引力的作用下发生了聚合，从而生成了一个足够大的球，是不是说明在其内部发生了行星核反应，进而转变成一个星球？没有理由相信我们能够如此的幸运，仅仅花费 7 年的时间就能够观察到一个星球转变成可见的状态，更不要说我们看到了两个！