在第4章中,我们讨论了能量守恒。在讨论中,我们没有使用牛顿定律,但是能量实际上是守恒的,遵从这些定律,我们非常感兴趣的是,它是如何得到的。为了澄清,我们应该从尽可能简单的情况开始,然后逐步深入。
最为简单的能量守恒的例子是一个垂直下落的物体,它仅在垂直方向上移动。在单独地引力的影响下,一个物体会改变它的高度,它有一个动能 $T$ (或者 $K.E.$ ),由它下落的运动产生,以及一个势能 $mgh$ ,简写为 $U$ (或者 $P.E.$ ),它们的和是一个常数:
\[\frac{1}{2}mv^2+mgh=const\]eq-13-1
\[T+U=const\]现在我们想要证明这个论点是正确的。说明它是对的,是什么意思?根据牛顿第二定律,我们可以很容易地讲述物体是如何运动的,很容易发现速度是如何随着时间变化,也就是,速度与时间成正比,高度随着时间的平方变化。如果我们从零点测量高度,物体起初是静止的,那么没什么惊奇的,高度会被证明等于速度的平方乘以一些常数。让我们再靠近一点。
根据牛顿第二定律,我们可以直观地得到动能是如何变化的,通过采用动能相对于时间的导数,再应用牛顿定律。当我们求导 $\frac{1}{2}mv^2$ 相对于时间,我们得到:
eq-13-2
\[\frac{dT}{dt}=\frac{d}{dt}(\frac{1}{2}mv^2)=\frac{1}{2}m2v\frac{dv}{dt}=mv\frac{dv}{dt}\]因为 m 被认为是常数。根据牛顿第二定律, $m(dv/dt)=F$ ,所以:
eq-13-3
\[dT/dt=Fv\]通常情况下,它应该是 $\boldsymbol{F}\cdot \boldsymbol{v}$ ,但是在这个一维的例子里,我们权当它是作用力乘以速度。
在我们简单的示例中作用力是常数,等于 $-mg$ ,一个垂直的作用力(负号表示它向下作用),以及速度,它是垂直位置的变化率,或者高度 h,伴随时间。因此动能的变化率是 $-mg(dh/dt)$ ,让人无比惊奇,该数值是负的某个其他东西的变化率!它是负的 $mgh$ 的时间变化率!因此,随着时间流逝,动能的变化与数值 $mgh$ 的变化相等且相反,所以这两个数值之和保持恒定,证明完毕。
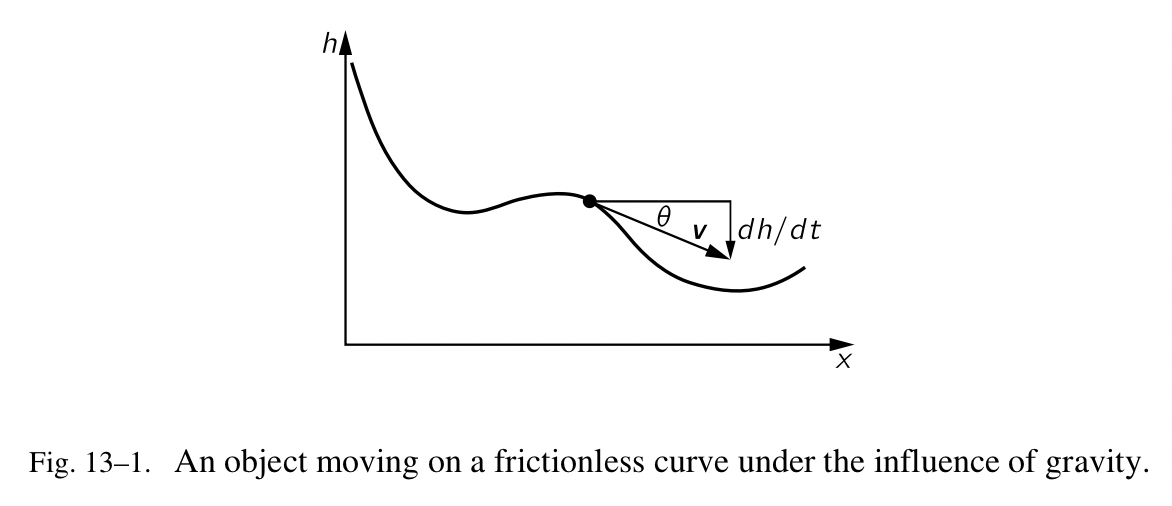
根据牛顿的运动第二定律,我们已经证明对于恒定的速度,能量是守恒的,当我们把势能 $mgh$ 与动能 $\frac{1}{2}mv^2$ 相加。现在让我们继续深入,看看它能否变得通用,从而提高我们的理解。难道它仅适用于自由下落的物体,或者它会更加通用?我们期望通过讨论,它可以适用于一个物体在引力的影响下,在某种无摩擦的曲线上,从一点移动到另外一点(Fig.13-1)。如果物体从原始的高度 H 到达一个特定的高度 h ,同样的公式再一次是正确的,即使速度现在是在某个方向上,而不是垂直的。我们想要弄明白为什么定律仍然是正确的。让我们遵循相同的分析,找到动能的时间变化率。它将再次是 $mv(dv/dt)$ ,但是 $m(dv/dt)$ 是动量的变化率,也就是,在运动方向上的作用力——切线作用力 $F_t$ 。因此
\[\frac{dT}{dt}=mv\frac{dv}{dt}=F_tv\]现在速率是沿着曲线的距离的变化率, $ds/dt$ ,切线作用力不是 $-mg$ ,而是比它弱,垂直的距离 $dh$ 与沿着路径的距离 $ds$ 的比值。
\[F_t=-mg\sin{\theta}=-mg\frac{dh}{ds}\]所以,
\[F_t\frac{ds}{dt}=-mg\frac{dh}{ds}\frac{ds}{dt}=-mg\frac{dh}{dt}\]因为 $ds$ 被抵消。因此我们得到 $-mg(dh/dt)$ ,它等于 $-mgh$ 的变化率,跟之前一样。为了完全理解能量守恒在力学的通用情况中是如何运作的,我们应该谈及一些概念,它们能够帮助我们分析。
首先,我们讨论在三维的通常情况中动能的变化率。在三维中的动能是
\[T=\frac{1}{2}m(v_x^2+v_y^2+v_z^2)\]当我们求导它相对于时间,我们得到了三个恐怖的元素:
eq-13-4
\[\frac{dT}{dt}=m(v_x\frac{dv_x}{dt}+v_y\frac{dv_y}{dt}+v_z\frac{dv_z}{dt})\]但是 $m(dv_x/dt)$ 是作用在物体上的在 x-方向上的力 $F_x$ 。因此等式 Fig.13.4 的右边是 $F_xv_x+F_yv_y+F_zv_z$ 。我们回忆一下向量分析,意识到它是 $\boldsymbol{F}\cdot \boldsymbol{v}$ ;因此
eq-13-5
\[dT/dt=\boldsymbol{F}\cdot \boldsymbol{v}\]这个结果可以通过下面的方式更快地得到:如果 $\boldsymbol{a}$ 和 $\boldsymbol{b}$ 是两个向量,它们或许都依赖于时间,在通常情况中, $\boldsymbol{a}\cdot \boldsymbol{b}$ 的导数是
eq-13-6
\[d(\boldsymbol{a}\cdot \boldsymbol{b})/dt=\boldsymbol{a}\cdot (d\boldsymbol{b}/dt)+(d\boldsymbol{a}/dt)\cdot \boldsymbol{b}\]假设 $\boldsymbol{a}=\boldsymbol{b}=\boldsymbol{v}$ ,于是我们可以应用它:
eq-13-7
\[\frac{d(\frac{1}{2}mv^2)}{dt}=\frac{d(\frac{1}{2}m\boldsymbol{v}\cdot \boldsymbol{v})}{dt}=m\frac{d\boldsymbol{v}}{dt}\cdot \boldsymbol{v}=\boldsymbol{F}\cdot \boldsymbol{v}=\boldsymbol{F}\cdot \frac{d\boldsymbol{s}}{dt}\]由于动能的概念,以及通常情况的能量,非常的重要,各种不同的名字被给出来,对应等式中的一些重要的元素,比如, $\frac{1}{2}mv^2$ 被称为动能。 $\boldsymbol{F}\cdot \boldsymbol{v}$ 被叫做功率:作用在一个物体上的力乘以该物体的速度(向量“点”积)是功率,由那个作用力转移给物体。因此我们有了一个很棒的理论:一个物体的动能的变化率等于作用其上的力做的功率。
为了学习能量守恒,我们想要更加深入地分析。让我们估算在很短的时间 $dt$ 内动能的变化。如果我们把等式13.7的两边都乘以 $dt$ ,我们发现在动能中的变化差是作用力“点”移动的距离差:
eq13-8
\[dT=\boldsymbol{F}\cdot d\boldsymbol{s}\]如果我们算积分,会得到:
eq-13-9
\[\Delta{T}=\int_1^2\boldsymbol{F}\cdot d\boldsymbol{s}\]它意味着什么?它表示如果一个物体在一个作用力的影响下以任意的方式运动,沿着某个曲线路径,当它沿着曲线从一点移动到另外一点,那么在动能中的变化等于作用力沿着曲线的部分乘以位移差 $ds$ 的积分,从一点到另外一点所涉及的积分。这个积分也有一个名字;它被叫做由物体上的作用力所做的功。我们立马可以看到功率等于每秒的做功。我们也看到仅仅是在运动方向上的作用力的一个部分贡献了做的功。在我们简单的例子中,作用力仅仅是垂直的,仅有一个单独的部分, $F_z$ ,等于 $-mg$ 。不管这个物体在那些情景中如何的运动,比如在一个抛物线上坠落, $\boldsymbol{F}\cdot \boldsymbol{s}$ ,可以被写作 $F_xdx+F_ydy+F_zdz$ ,什么都没留下,除了 $F_zdz=-mgdz$ ,因为作用力的其他部分都是零。因此,
eq-13-10
\[\int_1^2\boldsymbol{F}\cdot d\boldsymbol{s}=\int_{z_1}^{z_2}-mgdz=-mg(z_2-z_1)\]所以我们再次发现它仅仅是物体坠落的垂直高度,是势能的一部分。
有关单位的一个词语。因为作用力是以牛顿测量的,我们乘以一个距离获得功,功是以牛顿-米测量的( $N\cdot m$ ),但是大家不喜欢说牛顿-米,他们更喜欢说焦耳(J)。一牛顿-米被叫做一焦耳;功是以焦耳测量的。功率是焦耳每秒,它也被叫做一瓦特(W)。如果我们把瓦特乘以时间,结果是做的功。在我们屋子里由电力公司做的功,从技术上讲,等于瓦特乘以时间。这就是我们得到千瓦时的由来,1000 瓦特乘以 3600 秒,或者 $3.6\times 10^6$ 焦耳。
现在我们列举另一个能量守恒定律的示例。考虑一个物体,起初拥有动能,移动地非常快,它伴随着摩擦力在地板上滑动。它停了下来。一开始动能不是零,但是最终变为零;有作用力做功,因为只要有摩擦力,总是会有一个作用力的部分,它的方向与运动方向相反,所以能量会持续地减少。现在让我们把一个质量悬挂在一个固定点,使它在一个引力场中的垂直平面上摆动,没有摩擦力。在这儿发生的有些不同,因为当质量向上走,作用力向下,当它向下走,作用力还是向下。因此 $\boldsymbol{F}\cdot d\boldsymbol{s}$ 有一个符号向上,以及另一个符号向下。在向上和向下的路径上的每一个对应的点的 $\boldsymbol{F}\cdot d\boldsymbol{s}$ 的值完全相等且相反,所以积分的结果为零。因此回到底部的质量所拥有的动能与它离开时是一样的;这是能量守恒的原理。(注意,当有摩擦力存在时,能量守恒乍看之下是无效的。我们需要找到另一种能量。实际上,热量会在物体中产生,当它与另一个摩擦,但是在那一刻,或许我们意识不到。)