自然的法则可以从一些事实和封闭的逻辑推导当中提炼出来。
一个简单的杠杆装置
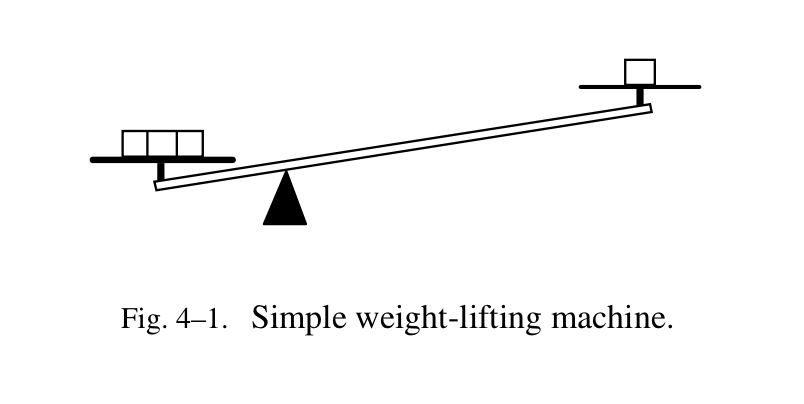
- 永动机并不存在,它是一个理想的装置,不需要借助外部的能量就能够保持自身地持续运转;
- 如图所示的装置可以被认为是一个可逆的装置,三单位重量的物体可以举起一单位重量的物体,那么反过来,一单位重量的物体可以举起三单位重量的物体;需要注意可逆的装置与永动机一样是想象出来,它是最有效的,因为现实的装置普遍都存在能量损耗的问题;
- 可以证明真实的装置举起物体的高度不可能超过可逆的装置举起物体的高度;
- 所有的可逆的装置举起物体的高度都是一样的,我们不需要关心其内部的细节。
一个稍微复杂点的可逆的装置
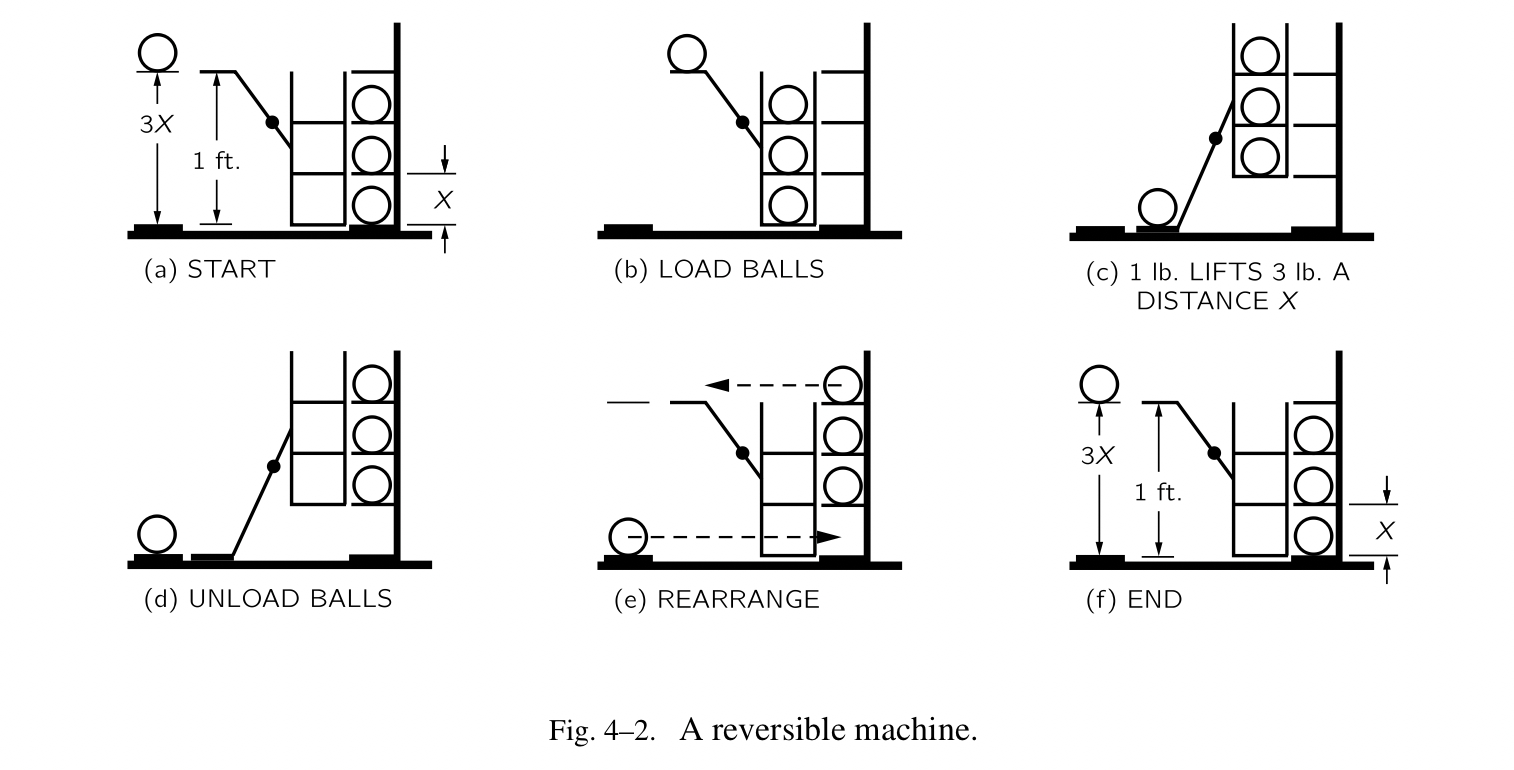
经过一系列的操作,我们发现:
- 1 英尺 = 3 X
- 另一个结论是,我们计算所有物体的重量乘以它们目前的高度,经由可逆的装置操作之后,把它们所有的重量再乘以结束时的高度,结果没有改变;
- 关于引力势能的公式:引力势能 = 重量 * 高度;
- 引力势能是物体在空间上相对于地球所拥有的能量;
- 势能是物体在当前位置相对于其他位置所拥有的能量。
直角三角形加滑轮的装置
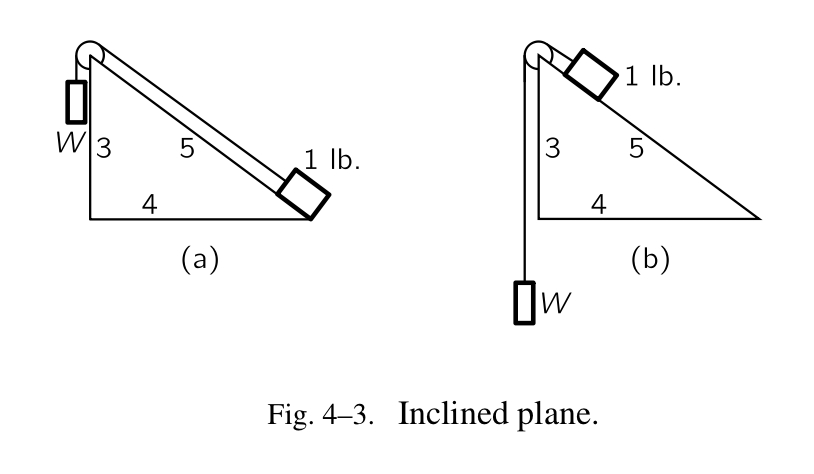
一个重量为 W 的物体下滑 5 英尺,举起了 1 英镑的物体 3 英尺,它们处于平衡的状态,我可以发现:
- W = 3 / 5 英镑
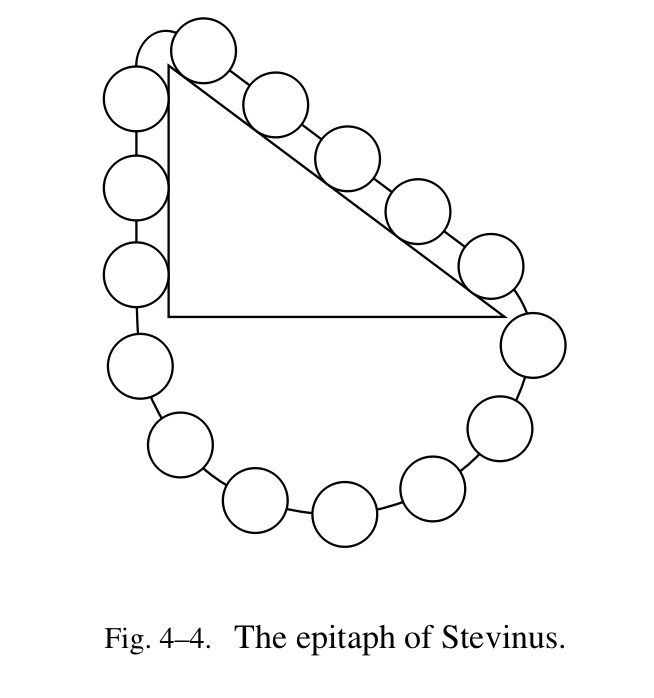
上图更加直观,左边三个链珠的拉力与右边五个链珠的拉力持平——整体处于平衡状态,不管余下链珠的占比如何。
另外两个较为复杂的可逆的装置
大螺丝
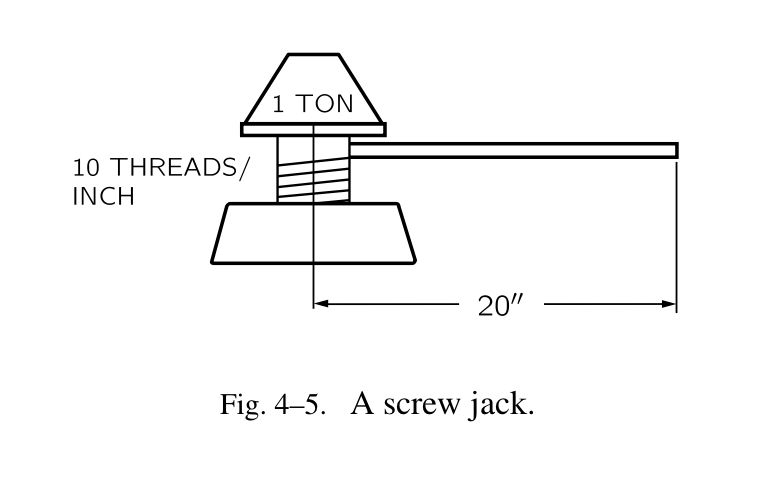
前置描述:
- 一个长柄 20 英寸,用于旋转螺丝;
- 螺丝沿着垂直方向位移 1 英寸需要旋转 10 圈;
问题是在长柄上需要多少力(假设为 W)才能够举起 1 吨重(大约 2000 英镑)的物体 1 英寸?
如果它可以被看作是可逆的装置,那么根据能量守恒定律,我们可以知道:
- W * 高度 = 2000 英镑 * 1 英寸
- 整体装置可以把它想象成一个简易的滑轮装置,左边重量为 W 的物体下滑了一定的距离(公式里的“高度”),举起右边 1 吨重的物体 1 英寸;
- 高度可以通过已知的信息计算出来:
- 注意长柄的位移方向是水平的;
- 20 英寸的长柄旋转一圈的长度为 2 * π * 20 英寸;
- 螺丝位移 1 英寸需要长柄转 10 圈,整体的长度为 2 * π * 20 英寸 * 10,约等于 1260 英寸;
- 代入公式,计算出 W 约为 1.6 英镑。
滑轮加多个物体
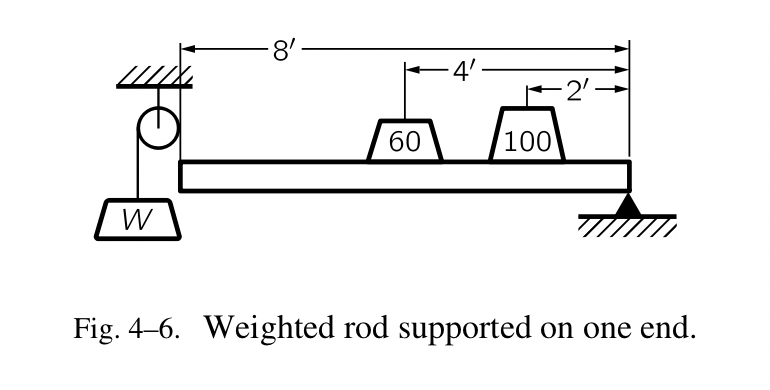
前置描述:
- 一个长条的一端被固定,该端点被称之为支点,长条的长度为 8 英寸;
- 长条的中间点上放置一个 60 英镑重的物体;
- 距离支点 1 /4 长条的长度的位置上放置一个 100 英镑重的物体;
- 忽略长条本身的重量;
问题是在滑轮的另一边需要多少力(假设为 W)才能够举起长条的另一端,从而让整体平衡?
- 我们已知 W 下滑了 4 英寸;
- 中间点放置的物体上升了 2 英寸,另一个物体上升了 1 英寸;
根据能量守恒定律,所有物体的重量与它们的高度的乘积的和不会改变,所以我们得到:
- -4 W + 2 * 60 + 1 * 100 = 0
- 计算出 W 为 55 英镑。
总结
只要真实的装置可以被归类于可逆的装置,那么我们就可以运用能量守恒定律计算需要的力的大小,可以把其想象成简单的杠杠装置或者滑轮装置,而不用关心其复杂的内部结构。