概率的点子非常有用，在描述一个气体样本中的 $10^{22}$ 或者如此多的分子的行为的情形里，对于试图写下每一个分子的位置或速度显然是不可实践的。当概率首次被应用到这样的问题，它被视为图方便——一种处理非常复杂情况的办法。我们现在相信概率的点子是描述原子级事物发生的本质。根据量子力学，粒子的数学理论，在位置和速度的详尽说明中总是会有某种不确定性。我们可以，最佳地，说有一个确定的概率——任意粒子将会拥有一个位置，接近某个坐标值 $x$ 。

我们可以给一个概率密度 $p_1(x)$ ，像这样的 $p_1(x)\Delta{x}$ 是粒子被发现介于 $x$ 和 $x+\Delta{x}$ 之间的概率。如果粒子被合理地安置，比如接近 $x_0$ ，函数 $p_1(x)$ 或许可以被视图 Fig.6-10(a) 给出。相似地，我们也可以由概率密度 $p_2(v)$ 的方式说明粒子的速度，其中 $p_2(v)\Delta{v}$ 是速度被发现介于 $v$ 和 $v+\Delta{v}$ 之间的概率。

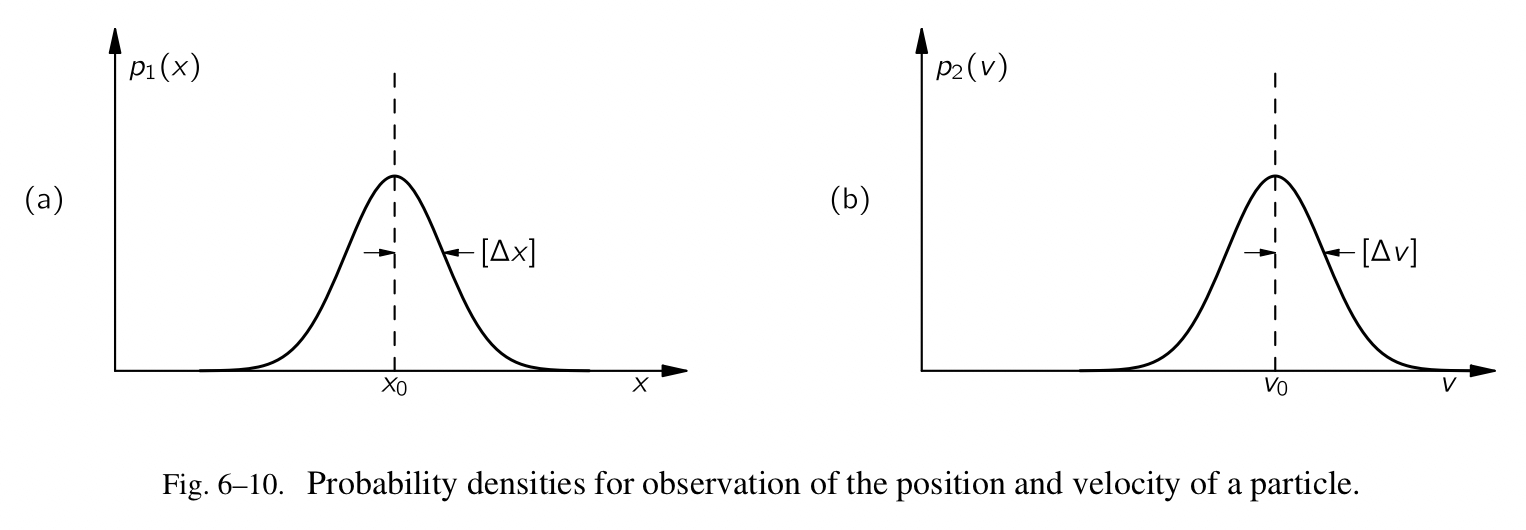
这是量子力学的基础的结果之一——函数 $p_1(x)$ 和 $p_2(v)$ 没有办法被独立地选定，实际上，它们也不能都被弄的很窄。如果我们把 $p_1(x)$ 的典型的“宽度”称为曲线 $[\Delta{x}]$ ，$p_2(v)$ 的称为曲线 $[\Delta{v}]$ （如图所示），自然要求两个宽度的乘积至少与数字 $\hslash/2m$ 一样大，其中 $m$ 是粒子的质量。我们也许可以把这个基础的的关系写成： \([\Delta{x}] [\Delta{v}]\geq{\hslash/2m}\)

这个等式是我们之前提过的海森堡不确定性原理。因为上面等式的右边是一个常数，这个等式说如果我们尝试“困住”一个粒子，通过强制它位于一个特定的位置，它最后会拥有一个很大的速度。或者如果我们尝试强制它变得很慢，或是一个精确的速度，它会“扩散”，所以我们没有办法很好地知道它刚刚在哪里。粒子总是以一种很有趣的方式行动。

不确定性原理描述了一种模糊的本质——它必然存在于任何尝试描述自然的情况里。我们对于自然的最精确的描述必须要涉及到概率。有一些人，他们不喜欢这种描述自然的方式。他们觉得只要他们可以说出粒子真正地将要发生什么，他们就能同时知道它的速度和位置。在量子力学发展的早期，爱因斯坦非常担心这个问题。他摇着脑袋说道：“但是，毋庸置疑，上帝不会扔骰子决定电子应该如何走！”他担忧了很长的时间，他也许从来都不会真正地让自己接受一个事实——这是人类能够给出的自然的最佳描述。仍然会有一个或两个物理学家，他们在直觉上坚信有可能通过另一种方式描述这个世界，那么所有的不确定性就能够被移除了。迄今为止还没有人可以成功。

必要的不确定性在我们对一个粒子的位置的详尽说明中变得最为重要，当我们希望去描述原子的结构。在氢原子中，一个质子的原子核带着在其外面的一个电子，不确定性在电子的位置中与原子自身一样大！我们不能，因此，正确地说电子是在某个轨道上围绕着质子移动的。我们最多能够说，有一个确定的机率 $p(r)\Delta{V}$ ，观察到电子在很小的体积 $\Delta{V}$ 中，位于距离质子为 $r$ 的位置上。概率密度 $p(r)$ 是由量子力学给出的。对于一个没有干扰的氢原子 $p(r)=Ae^{-2r/a}$ 。数字 a 是一个“典型的”半径，其函数会迅速地减小。因为找到电子位于距离原子核比 $a$ 更大的位置上的概率很小，我们也许可以认为 $a$ 是“原子半径”，大约 $10^{-10}$ 米。

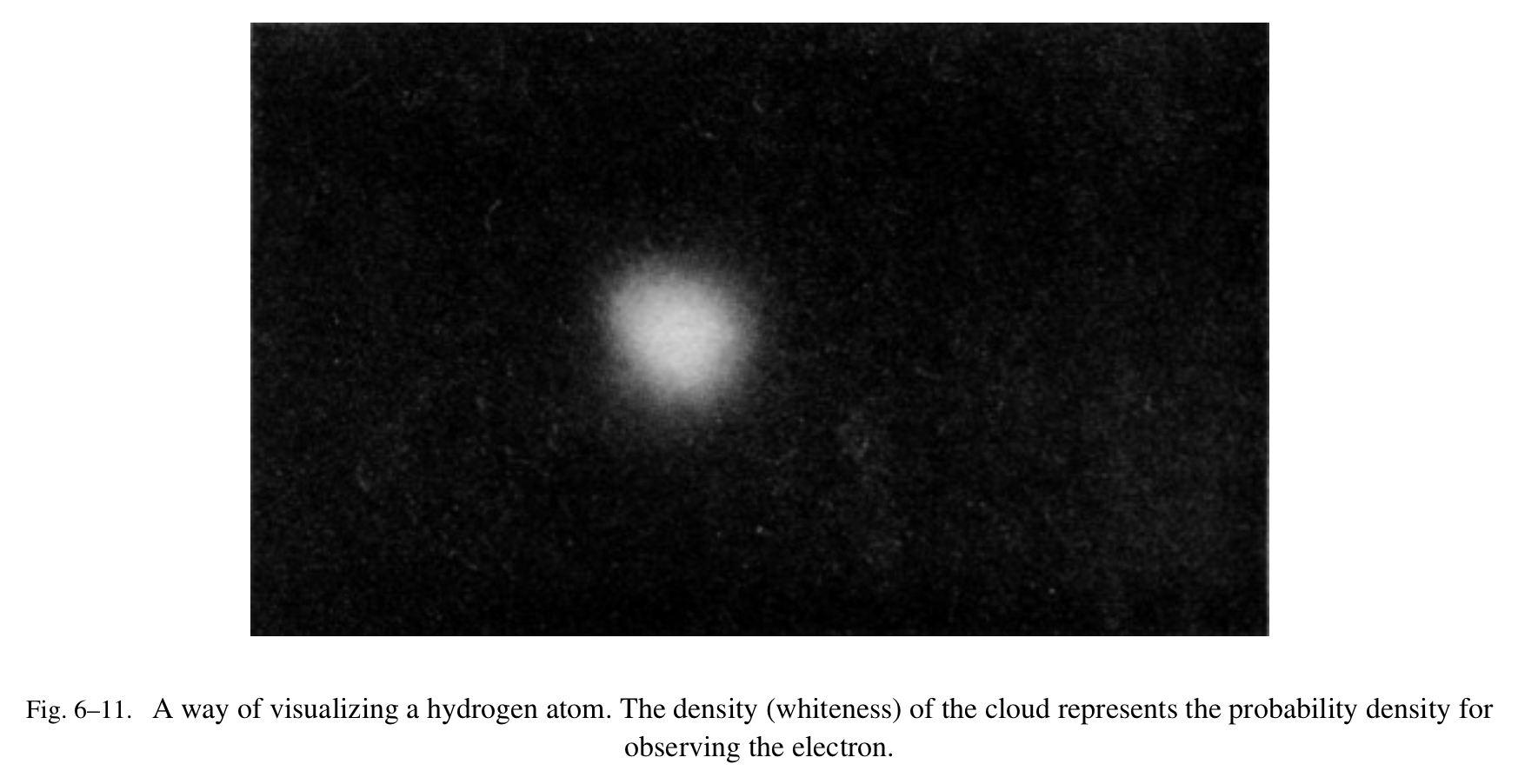
我们可以形成一个氢原子的画面通过想象一个“云团”，它的密度与观测到的电子的概率密度成正比。像这样的一个云团样本如图 Fig.6-11 所示。一个氢原子的最佳“图片”是一个原子核被电子云团包围（尽管我们真正想说的是一个“概率云团”）。电子是在某个地方，但是自然仅仅允许我们知道找到其位于任意特定位置的机率。

在努力学习了尽可能多的关于自然的知识之后，现代物理发现确定的事物从来都不能被确定的“知道”。我们许多的知识都必须保有不确定性。大部分我们可以了解的都涉及到概率。