正如之前所说的,大家曾经尝试使用“以太”假说去确定地球的绝对速度,以太曾被认为是无处不在的。其中最著名的实验是由迈克耳孙和莫雷在 1887 年做的。该实验的负面结论最终由爱因斯坦在 18 年后解释。
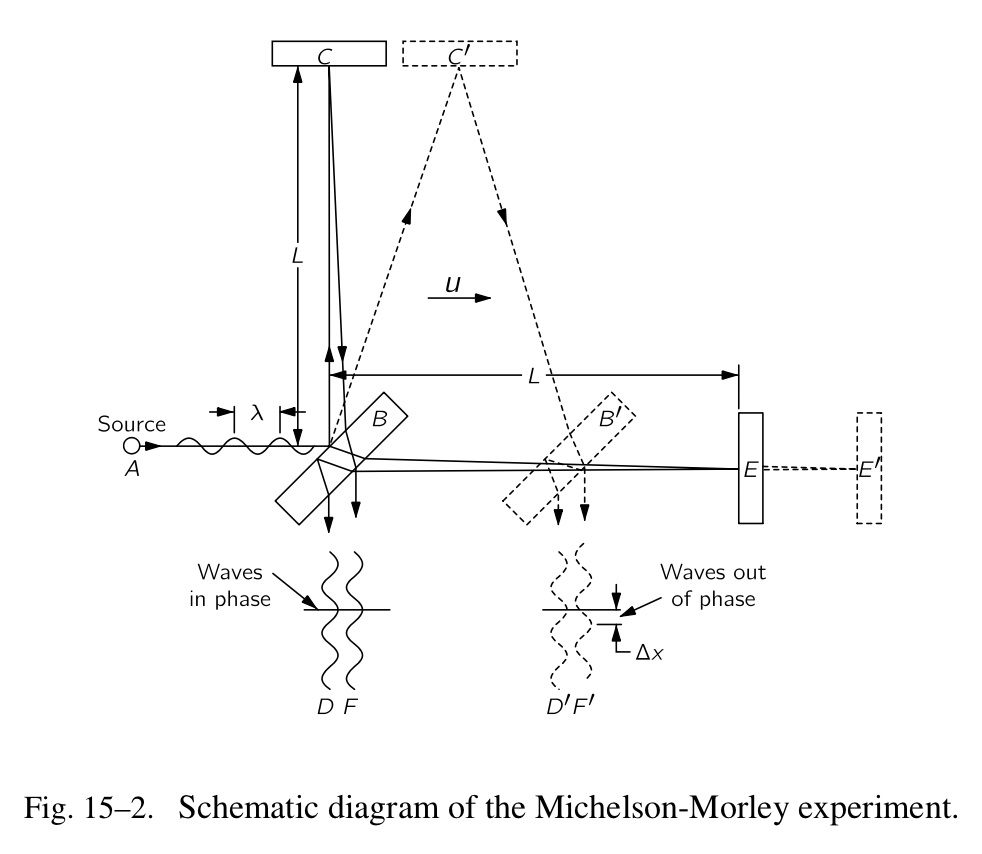
迈克耳孙-莫雷实验的装置如图 Fig.15-2 所示。该装置是由一处光源、一块部分镀银的玻璃片 B、两个镜子 C 与 E 构成,所有的部件都被固定在不可移动的结构上。镜子分别被放置在距离 B 长度为 L 的位置。玻璃片 B 把迎面而来的光拆分成两束,它们分别沿着垂直于镜面的方向继续运动,经反射再返回到 B 。在抵达 B 处,两束光再次合并,就像两束叠加的光,D 和 F 。如果光从 B 到 E 再返回所花的时间与它从 B 到 C 再返回所花的相同,光束 D 和 F 将会同步,它们彼此会增强,但是如果两个时间稍有不同,光束不会同步,干扰将会发生。如果装置在以太中是“静止的”,时间应该是完全地相同,如果它以一个速度 u 向右边移动,在时间上应该会有所不同。让我们看看这是为什么。
首先,让我们计算光从 B 到 E 再返回所需要的时间。我们说,光从玻璃片 B 到镜子 E 所需要的时间是 $t_1$ ,返回所需要的时间是 $t_2$ 。当光从 B 到达 E ,装置移动了一段距离 $ut_1$ ,那么光移动的距离一定是 $L+ut_1$ ,速率是 c 。我们也可以把这段距离表示为 $ct_1$ ,因此我们得到
\[ct_1=L+ut_1, \quad or \quad t_1=L/(c-u)\](从此也可以很明显地看出光相对于装置的速度是 $c-u$ ,所以时间是长度 L 除以 $c-u$ 。相似的,时间 $t_2$ 也可以被计算。在这段时间期间,玻璃片 B 移动了一段距离 $ut_2$ ,所以光返回的距离是 $L-ut_2$ 。于是我们得到
\[ct_2=L-ut_2, \quad or \quad t_2=L/(c+u)\]整体的时间是
\[t_1+t_2=2Lc/(c^2-u^2)\]为了方便后面的时间比较,我们把它写作
eq-15-4
\[t_1+t_2=\frac{2L/c}{1-u^2/c^2}\]第二个需要计算的是光从 B 到镜子 C 所花费的时间 $t_3$ 。像之前一样,在时间 $t_3$ 期间,镜子 C 向右移动了一段距离 $ut_3$ 到达位置 $C’$ ;与此同时,光移动了一段距离 $ct_3$ ,沿着一个三角形的斜边 $BC’$ 。对于这个直角三角形,我们可得
\[(ct_3)^2=L^2+(ut_3)^2\]或者
\[L^2=c^2t_3^2-u^2t_3^2=(c^2-u^2)t_3^2\]从中我们可以得到
\[t_3=L/\sqrt{c^2-u^2}\]对于从 $C’$ 的返程,距离是相同的,就像我们在对称的图形中所看到的;因此返回的时间也是相同的,整体的时间是 $2t_3$ 。我们对它稍作修整
eq-15-5
\[2t_3=\frac{2L}{\sqrt{c^2-u^2}}=\frac{2L/c}{\sqrt{1-u^2/c^2}}\]我们现在可以比较两束光所花费的时间。在表达式 15.4 和 15.5 中分子是相同的,表示在装置静止时所花费的时间。在分母中,元素 $u^2/c^2$ 会很小,除非 u 可以与 c 进行比较。分母表示在时间上的改变,由装置的运动所致。这些改变并不相同——到 C 再返回所用的时间要比到 E 再返回所用的少一点,即使镜子到 B 的距离是相等的,需要我们做的就是测量精度的差异。
这里有一个不是那么重要的技术点——假设两个长度 L 不是完全地相等?实际上,我们可以确信无法让它们完全相等。在示例中,我们简单地把装置旋转 90 度,好让 BC 处于运动的线上,BE 垂直于运动。任何细小的差异在长度上变得无关紧要,我们想要看到的是当我们旋转装置时在干涉条纹上的变化。
在做的实验中,迈克耳孙和莫雷转动装置,好让线 BE 几乎与地球在它的轨道上的运动平行(在白天和黑夜的确定的时间)。轨道的速度大概是 18 英里每秒,任何的“以太运动”至少应该是这么多,在白天和黑夜的某个时间以及在一年的某个时间。装置非常敏感,可以观测到这样的效果,但是没有发现任何时间的差异——地球通过以太的速度无法被检测到。实验的结果是无效的(零结果)。
迈克耳孙-莫雷的实验结果令人感到困惑和沮丧。第一个提出解决之道的是洛伦兹。他提出材料本身会缩小,当它们移动时,并且这种减少只会出现在运动的方向上,当它处于静止时,如果长度是 $L_0$ ,那么当它以速率 u 平行于它的长度运动时,新的长度,我们叫做 $L_{\parallel}$ (L-平行),它是
eq-15-6
\[L_{\parallel}=L_0\sqrt{1-u^2/c^2}\]当这个修正被应用到迈克耳孙-莫雷干涉测量装置上,由 B 到 C 的距离不会改变,但是由 B 到 E 的距离缩减为 $L\sqrt{1-u^2/c^2}$ 。因此等式 15.5 不会改变,但是等式 15.4 的 L 必须根据等式 15.6 进行修正。当完成后,我们得到
eq-15-7
\[t_1+t_2=\frac{(2L/c)\sqrt{1-u^2/c^2}}{1-u^2/c^2}=\frac{2L/c}{\sqrt{1-u^2/c^2}}\]将结论与等式 15.5 进行比较。如果装置以刚刚描述的方式缩小,我们可以理解迈克耳孙-莫雷实验为什么毫无效果。虽然缩小假说成功地解释了实验的负面结论,但是它引起了争议,它的发现纯粹是为了逃避困难,过于刻意。然而在发现以太风的其他实验中,相似的困难会出现,自然似乎在酝酿一场“阴谋”来阻止人类前行,通过引入某些新的现象打消他以为所有的现象允许测量 u 的念头。
最终由庞加莱指出,这场阴谋本身就是一条自然定律!庞加莱提出有这样一条自然定律,不可能通过任何实验发现以太风;也就是,没有方法可以确定绝对速度。