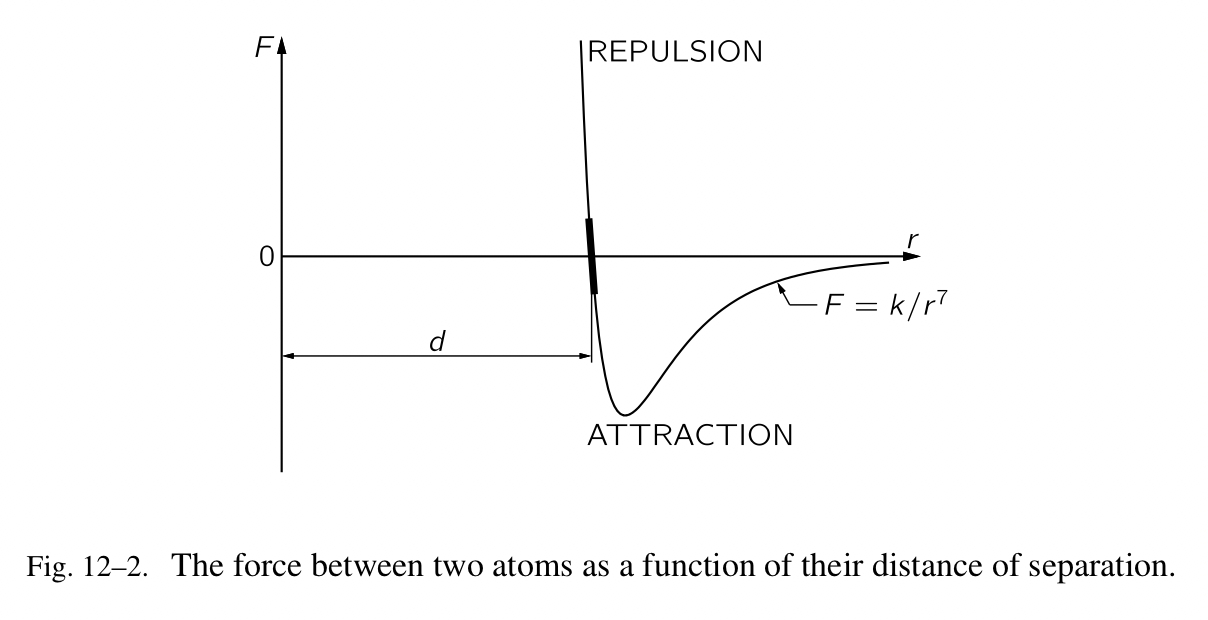
接下来我们会讨论分子作用力的特征。它们是原子之间的作用力，是最原始的摩擦力。分子作用力在基础的经典物理上从来都没有被很好地解释；需要引入量子力学才能完整地理解它们。不过，通过实验，原子之间的作用力可以由 Fig.12-2 表示，其中两个原子之间的作用力 F 被绘制为它们之间的距离 r 的一个函数。存在不同的情况：在水分子中，负电荷更多的坐落在氧元素上，负电荷的平均位置与正电荷的平均位置不相同；由此导致的是，附近的另一个分子感受到一个相当大的作用力，被称之为偶极-偶极作用力。然而，对于很多系统，电荷平衡地很好，尤其是氧气，它完美对称。在这种情况里，虽然负电荷和正电荷遍布分子各处，分布的情况是负电荷的中心与正电荷的中心重合。中心不重合的分子被称为极性分子，电荷乘以中心之间的距离被称为偶极矩。非极性分子的电荷中心重合。对于所有的非极性分子，所有的电子作用力都被中和，不过它仍然可以证明在很远处的作用力是一个吸引力，它与距离的七次方成反比，也就是 $F=k/r^7$ ，其中 k 是一个常数，取决于分子。想要一探究竟，只能在了解量子力学以后。当有电偶极时，作用力会更大。当分子或原子靠的太近，它们会产生一个非常大的互斥力，这就是为什么我们没有坠入地板之中。

这些分子作用力可以直接阐述：一个是滑动玻璃杯的摩擦实验；另一个是两个精细加工的表面，它们非常平整，表面能够贴合在一起。像这种表面的示例是块规，在机械店中，被用作精确测量长度的标准件。如果一个块件在另一个上被仔细地滑动，举起上面的，另一个也随之举起，由于分子的作用力，这表明一个块件上的原子对另一个的原子存在吸引。

这些分子的吸引力并不是基础的（引力是基础的）；它们由非常复杂的交互所致——一个分子的所有电子和原子核与另一个的所有电子和原子核。任何看似简单的公式是复杂性的一个集合，因此我们还未看到基础现象。

因为分子的作用力在远处吸引、在近处互斥，如图 Fig.12-2 所示，我们可以构造固体，通过吸引力让原子聚拢，当它们靠太近时，通过互斥力让彼此分离。在一个确定的距离 d 处（在 Fig.12-2 中的线条穿越坐标轴的地方）作用力为零，意味着它们都被平衡了，分子与另一个保持那段距离。如果分子被推动的靠近彼此的距离小于 d，它们则都是互斥力，由 r-轴上面的图表部分表示。仅仅推动一点儿需要巨大的作用力，因为分子的互斥力在小于 d 处迅速地增长。如果分子被拉开一点儿，有一个微弱的吸引力，它随着距离的增加而增加。如果它们被拉的够狠，它们会永久分离——连接被破坏。

如果分子被推动的，或者拉开的是很小的距离，在 Fig.12-2 中的曲线上对应的距离也会很小，可以近似为一条直线。因此，在很多情形中，如果位移不是太大，作用力与位移成正比。这则原理被称为胡克定律，或者弹性定律，说的是当一个物体产生形变时，其自身尝试恢复到初始状态的作用力与形变成正比。这条定律，只有在形变非常小时才是对的，如果它太大，物体会裂开，或者被毁坏，这取决于具体的形变；多大的作用力才适合胡克定律，取决于材料；比如，对于面团、油灰作用力很小，但是对于钢铁它很大。我们可以通过弹簧很好地解释胡克定律，它由钢制成，垂直悬挂。悬挂于弹簧底部的一个适量的重物会产生一丁点扭力，遍及全身，它会导致每一圈的垂直方向上发生细微变化，加在一起就是一个大的位移，如果有很多圈儿的话。我们悬挂 100 克重量，测量其延长了多少，我们发现每增加 100 克都会有额外的延长，它跟我们首次测量 100 克的几乎一样。作用力相对位移的恒定比开始改变，当弹簧超过负载，胡克定律不再有效。