作用力和功的另一个特性是：假设我们有一个倾斜的或者弯曲的轨道，一个物体必须要沿着轨道运动，但是没有摩擦力。或者，我们有一个摆，一条线连着一个重物；这条线限制着物体做围绕固定点的环形运动。固定点或许会改变，在它碰到一个挂钩，路径会变为两个不同半径的圆。这些例子我们称其为固定的、无摩擦的限制。

在一个固定的、无摩擦的运动中，限制不做功，因为限制的作用力总是垂直于运动。我们说的“限制的作用力”，指的是那些直接作用在物体上的作用力——与轨道接触的作用力，或者绳子的张力。

在引力的作用下在一个斜面上移动的一个粒子的运动中包含的作用力相当的复杂，因为有一个限制作用力、一个引力作用力，等等。然而，如果我们基于能量守恒和单独的引力作用力去计算运动，我们会得到正确的结果。这看起来相当的奇怪，因为它不是严格地以正确的方式去做的——我们应该使用全部的作用力。由引力单独做的功被证明是动能的变化，因为由作用力的限制部分所做的功为零（Fig.14-1）。

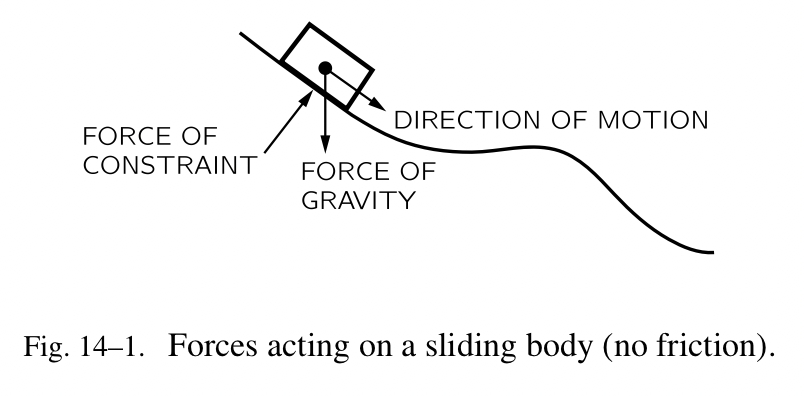
这儿的重点是如果作用力可以被当作是两片儿或更多片儿的和去分析，那么在一个确定的曲线上由整体作用力所做的功是当作各种部分被分析的作用力所做的功的和。因此如果我们可以把作用力当作是几个效果的向量的和去分析，引力加上限制作用力，或者全部作用力的 x-部分、全部作用力的 y-部分，或者依我们所愿拆分成其他的任意方式，那么由净的作用力所做的功等于我们在分析中把作用力拆分的全部的部分所做的功的和。