接下来我们要讨论的作用力或许可以叫做假想力。在第11章，我们讨论过两个人之间的关系，乔和莫，他们使用不同的坐标系。让我们假设由乔测量的粒子的位置是 $x$ ，由莫测量的是 $x^{‘}$ ；然后定律如下：

\[x=x^{'}+s,\quad y=y^{'},\quad z=z^{'}\]

其中 s 是莫的系统相对于乔的位移。如果我们假设运动定律对于乔是无误的，那对于莫看来如何？我们首先发现：

\[dx/dt=dx^{'}/dt+ds/dt\]

之前我们考虑过 s 是常数的情况，我们发现 s 没啥作用，在运动定律中，因为 $ds/dt=0$ ；最终，物理定律在两个系统中都是一样的。但是另一个情况，我们会采纳 $s=ut$ ，其中 u 是一条直线上的恒定速度。因此 s 不是恒定的， $ds/dt$ 不等于 0，但是 u 是一个常数。加速度 $d^2x/dt^2$ 与 $d^2x^{‘}/dt^2$ 相同，因为 $du/dt=0$ 。它证明了第10章中我们运用的定律，也就是当我们在直线上以恒定的速度移动，物理定律与我们处于静止时是相同的。这是伽利略变换。但是我们想讨论有趣的案例，其中 s 更加复杂，如 $s=at^2/2$ 。然后 $ds/dt=at$ ， $d^2s/dt^2=a$ ，一个恒定的加速度；或者在一个更加复杂的案例中，加速度是一个时间函数。这表明从乔的视野看，运动定律是

\[m\frac{d^2x}{dt^2}=F_x\]

从莫的视野看，运动定律是

\[m\frac{d^2x^{'}}{dt^2}=F_{x^{'}}=F_x-ma\]

因为莫的坐标系相对乔的正在加速，额外的元素 ma 出现了，莫需要用那个数值修正他的作用力，来让牛顿定律奏效。也就是说，这儿有一个神秘的新作用力，从未知的源产生，是由于莫没有正确的坐标系。这是一个假想力的示例，另一个出现在旋转中。

另一个假想力的示例通常被称为“离心力”。在一个旋转坐标系中的观察者，比如，在一个盒子里，将会发现神秘的作用力，不是来自任何已知的作用源，把东西摔在墙上。这些作用力主要是由于观察者没有牛顿的坐标系（它是最简单的坐标系）导致的。

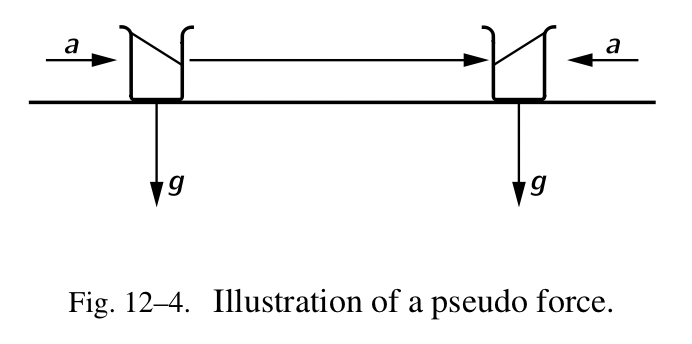
假想力可以由一个趣味实验描述，我们沿着桌面推一杯水，带加速度。引力当然是向下作用在水上，但是由于水平的加速度，也会存在一个假想力在水平位置，它的方向与加速度相反。全部的引力、假想力与垂直方向形成一个夹角，在加速期间，水面与整个作用力垂直，也就是，与桌面倾至一个角度，水的高位处于容器后边。当停止推杯子，杯子由于摩擦减速，假想力反转，水的高位处于容器前边（Fig.12-4）。

假想力的一个重要特征是它们总是与质量成正比；引力也是一样。可能性是存在的，引力自身是一个假想力。难道引力不是由于我们没有正确的坐标系所以产生的吗？我们总是可以得到一个作用力正比于质量，如果我们想象一个物体正在加速。比如，一个人被关在地球上的一个盒子里，盒子是静止的，他发现自己在盒子的底部，因为一个作用力，它与他的质量成正比。但是如果没有地球，盒子是静止的，那么人会漂浮在空中。另一方面，如果没有地球，某种东西以加速度 g 拉拽盒子，盒中人作物理分析，会发现一个假想力，把自身维系在地板上，如同引力。

爱因斯坦提出了著名的假说，加速度可以模拟引力，加速度的作用力（假想力）无法从那些引力中辨别，根本说不清它们有多少是引力，有多少是假想力。

看起来把引力当作是假想力没啥毛病，我们之所以被向下维系是因为我们正在向上加速，那么地球的另一边呢，马达加斯加的人们也是正在加速吗？爱因斯坦发现引力只有在时间的某个点上才能被当作是假想力，由此他提出这个世界的几何要比欧几里得几何复杂得多。当前的讨论是非量化的，并没有比通用的概念提供更多的解释。给一个粗略的观点，为何引力是假想力的产物，我们用纯几何的方式论述，它无法代表真实的情况。假设我们都居住在二维里，不知道第三维。我们认为我们是在一个平面上，但是假设我们真的是在一个球面上。如果我们沿着地表射出一个物体，没有力作用其上。它会去哪儿？它看起来走的是直线，但是会停在球面上，两点之间的最短距离沿着的是一个大圆；所以它绕着一个大圆运动。相似的，如果我们朝另一方向射出一个物体，它会绕着另一个大圆运动。因为我们认为我们是在一个平面上，所以我们预期这两个物体随着线性时间的增加会分得越来越远，但是仔细地观察表明如果它们走的足够远，它们会再次靠的更近，就好像它们彼此吸引。但是它们并没有彼此吸引，这个几何真的“很奇怪”！上面的论述没有说清爱因斯坦的几何怪在哪儿，而是说如果我们充分地改变几何，所有的引力说不定都是以某种方式与假想力相关；这是爱因斯坦引力理论的主要观点。