让我们再进一步探索。

如果扔出硬币 N 次，那么我们期望得到正面的次数是多少？

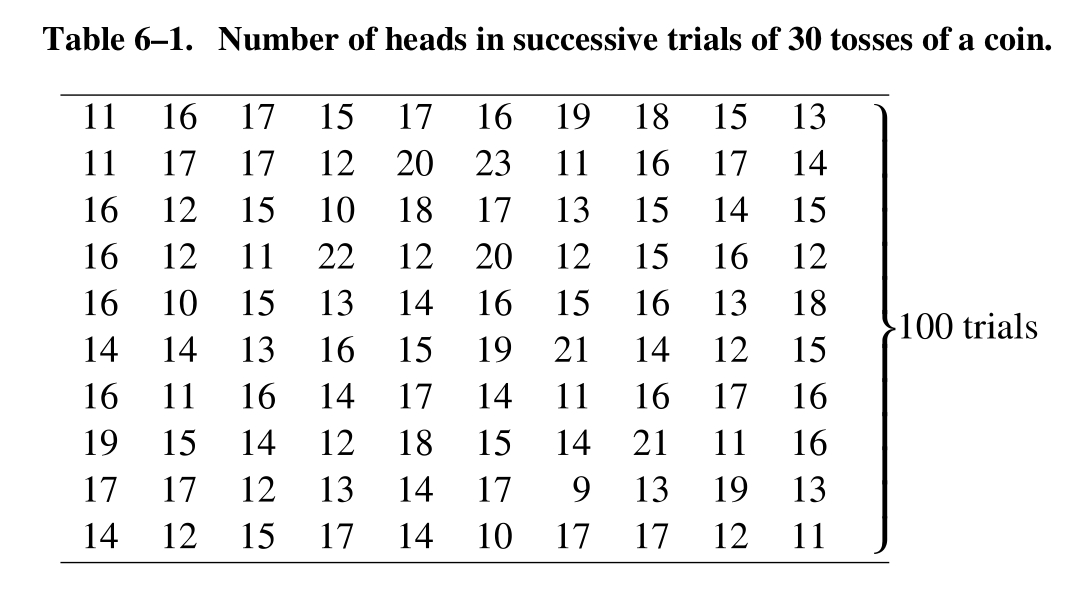
我们进行100组抛掷硬币的测试，每组抛掷30次，上图统计的是每组出现正面的次数。我们发现大部分的结果接近数字“15”，它们介于12到18之间。如果我们可以用图形展示这些结果的分布，就能够获得更直观的感受。

fig-6-2

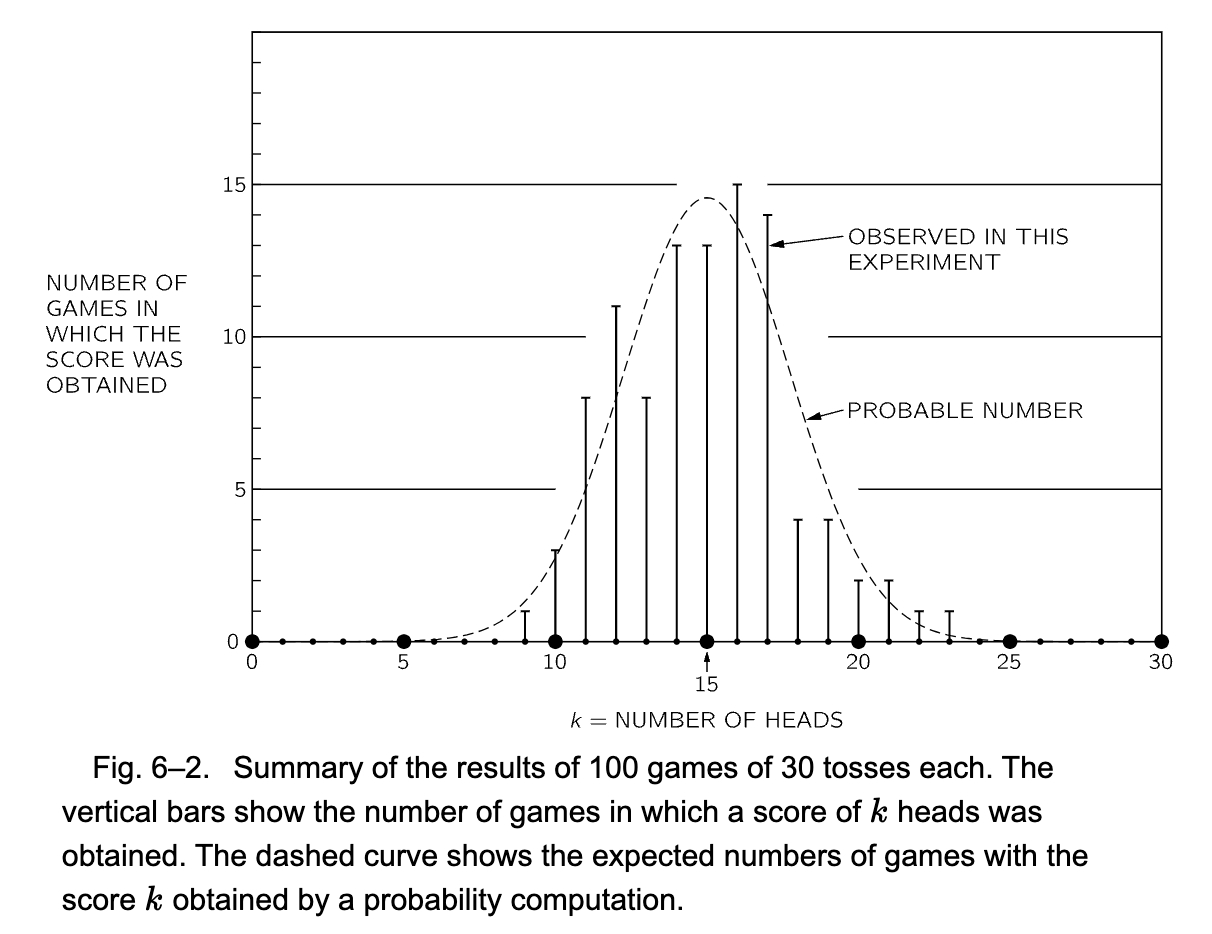
x 轴表示每组出现正面的次数，设置为 k，y 轴表示出现 k 的游戏计数，图中的虚线表示通过概率计算得到的出现 k 的游戏计数。在一共 3,000 次抛掷中，出现正面的次数为 1,493 次，出现正面的占比为 0.498，非常接近一半。我们注意到正面出现 16 次的游戏计数为 15，是最高的，这是一个真实的“意外”，我们依然预期最有可能出现正面的次数为 15。

在这个抛掷硬币 30 次的游戏里，正面出现 15 次，或 16 次，或任意一个数字的概率是多少？

设置 H 表示硬币正面，T 表示背面。在两次抛掷硬币的结果中有四种可能，HH、HT、TH、TT，我们可以总结：

• 出现两次正面的概率为 $\frac{1}{4}$ ；
• 出现一次正面的概率为 $\frac{2}{4}$ ；
• 出现零次正面的概率为 $\frac{1}{4}$ ；
• 出现一次正面的结果有两种，分别为 HT、TH；
• 出现两次正面的结果或零次正面的结果仅有一种；

如果是三次抛掷，我可以采用下面的形式进行展示：

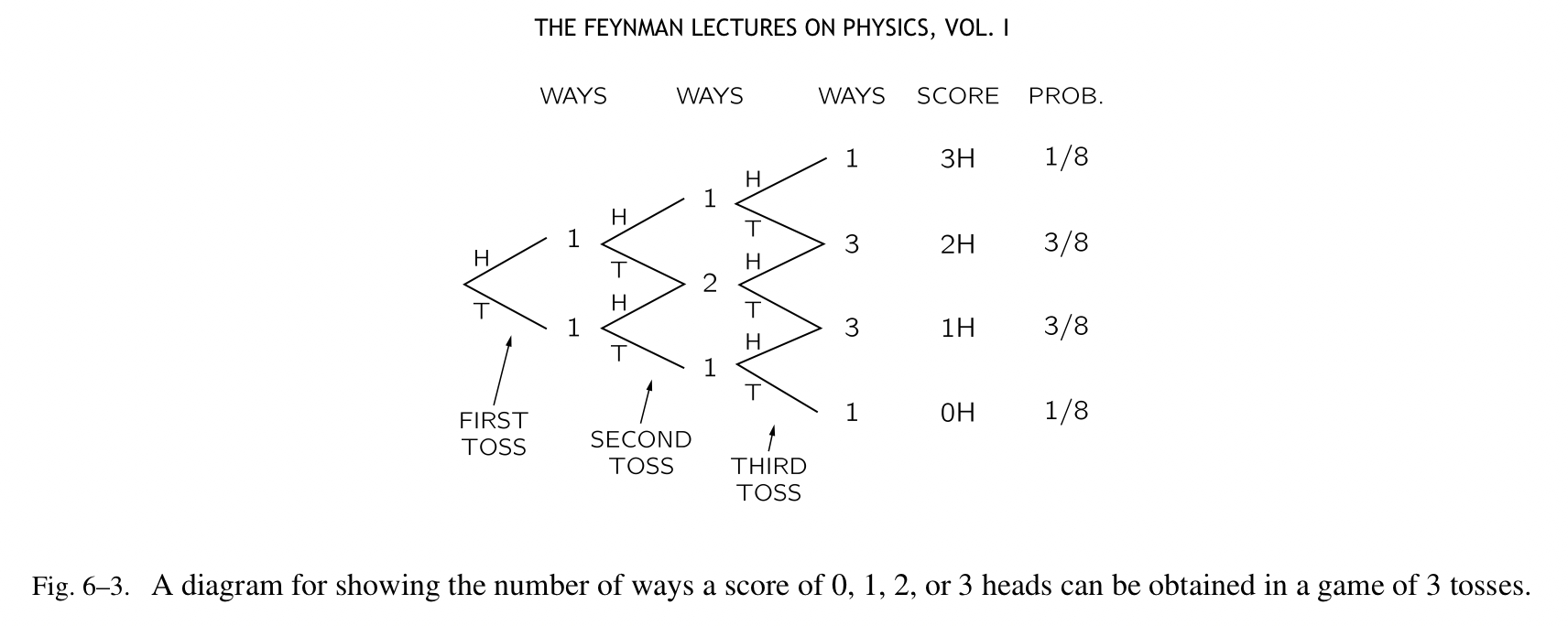
在图表的“ways”列中，任意一个数值表示从第一次抛掷到本次抛掷可能出现的结果种数（对应于相同行的“score”列的值）。我们进行6次抛掷，把图表进行部分简化得到：

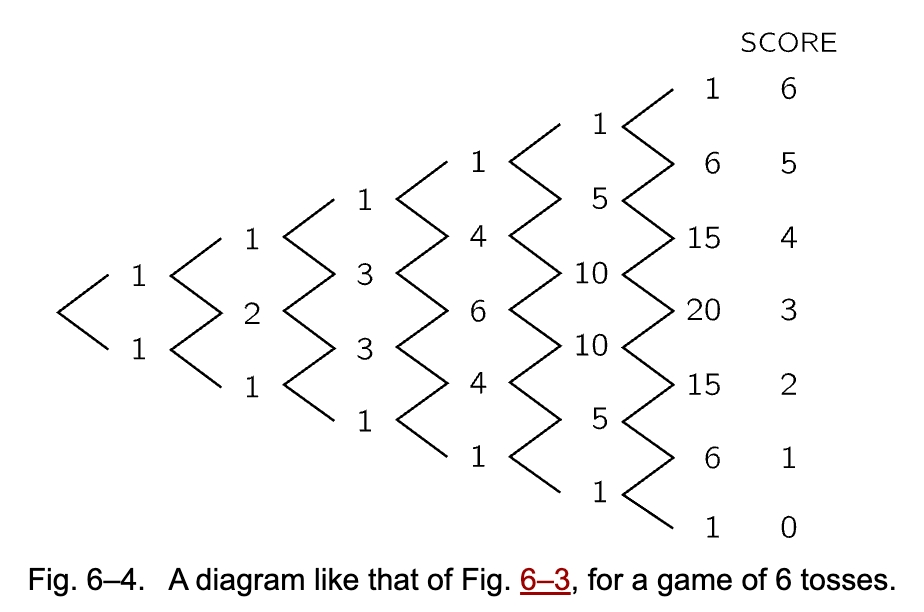
图表中的数字组合契合帕斯卡三角形，同样也适用于二项式系数。如果我们把抛掷的总次数设置为 n，出现正面的次数设置为 k，那么图表中“ways”列的值通常可以被表示为 $(^n_k)$，公式如下： \((^n_k) = \frac{n!}{k!(n - k)!}\)

• n! 表示 n 的阶乘；

我们现在可以计算在 n 次抛掷中出现 k 次正面的概率—— $P(k,n)$ ，已知在所有的抛掷中可能出现的结果种数为 $2^n$ ，那么： \(P(k,n) = \frac{(^n_k)}{2^n}\)

因为 $P(k,n)$ 是在一次游戏中（n 次抛掷）我们预期出现 k 次正面的结果计数的占比，那么在 100 次游戏中我们预期出现 k 次正面的游戏计数为 $100 * P(k,n)$ ，Fig. 6-2 的曲线就是通过 $100 * P(k,30)$ 计算得到的。我们预期出现15次正面的游戏计数为 14 或 15，而实际上我们观察到的游戏计数为 13；我们预期出现 16 次正面的游戏计数为 13 或 14，实际上并不是，这样真实的的“意外”是游戏的一部分。

上述方法可以应用于大部分情况，只要是一次观察仅可能出现两种结果，比如赢（W）或输（L）。通常情况下，赢和输的概率在一次事件中并不需要相等，我们用 p 表示赢的结果出现的概率，q 表示输的概率， $1 - p$ 。那么在 n 次测试中，赢的结果出现 k 次的概率为： \(P(k,n) = (^n_k)p^kq^{n-k}\)

概率函数被称之为伯努利，或者二项分布。