我们刚刚做的东西在数学里很普遍，为方便起见，我们把特殊符号 $\epsilon$ 和 $x$ 分配在数值上。在这个表示里， $\epsilon$ 变成了 $\Delta{t}$ ， $x$ 变成了 $\Delta{s}$ 。 $\Delta{s}$ 表示“t 额外多出了一点”，隐含的信息是它可以变得更小。前缀 $\Delta$ 不是乘法，就像 $\sin\theta$ 不是 $s\cdot{i}\cdot{n}\cdot{\theta}$ 。它简单地表示时间增加，提醒我们它是一个特殊的符号。 $\Delta{s}$ 类比于距离 $s$ 。因为 $\Delta$ 不是一个因子，它不能在占比 $\Delta{s}/\Delta{t}$ 中取消变成 $s/t$ ，就像 $\sin{\theta}/\sin{2\theta}$ 不能简写成 $1/2$ 一样。在这个表示里，速度等于 $\Delta{s}/\Delta{t}$ 的极限，当 $\Delta{t}$ 变得更小，或者

\[v=\lim_{\Delta{t} \to 0}\frac{\Delta{s}}{\Delta{t}}\]

这个跟我们之前的表达式是一模一样的，就是那个带着 $\epsilon$ 和 $x$ 的（Eq.8.3），但是它的优势在于显示出某些东西正在改变，以及追踪它的改变。

基于不错的近似，我们有了另一个定律，它说一个移动点在其位置上的改变是速度乘以时间间隔，或者 $\Delta{s}=v\Delta{t}$ 。这个表述是对的仅仅在速度于时间间隔内不会发生改变，这个条件是对的仅仅在伴随着 $\Delta{t}$ 变为 0 的极限内。物理学家喜欢写作 $ds=vdt$ ，因为他们说的 $dt$ 表示在所述的场景中 $\Delta{t}$ 非常的小；基于这些理解，该表达式可以成为很棒的近似。如果 $\Delta{t}$ 太长，速度可能会在期间改变，近似就变得不精确了。对于时间 $\Delta{t}$ ，越趋近于 0 ， $ds=vdt$ 越精确。在这个表示中我们可以写作

\[v=\lim_{\Delta{t} \to 0}\frac{\Delta{s}}{\Delta{v}}=\frac{ds}{dt}\]

上面的数值 $ds/dt$ 被称之为 s 相对于 t 的导数（语言表达出追踪了什么的改变）。寻找这个复杂的过程被称之为寻导或求导。 $ds$ 和 $dt$ 独自出现，我们叫它微分。组织一下语言，我们说函数 $16t^2$ 的导数或者 $16t^2$ （相对于 t）的导数是 $32t$ 。当我们使用这些表达，该类点子更容易被理解。让我们操练起来，寻求一个更加复杂的函数的导数。我们应该考虑公式 $s=At^3+Bt+C$ ，它也许描述的是一个点的运动。字母 A、B以及 C表示常数，就像普遍的一元二次方程。从运动的等式开始，我们希望求得任意时间点的速度。为了采用更加优雅的方式，我们把 t 变成 $t+\Delta{t}$，s 变成 $s+$ 一些 $\Delta{s}$ ；然后我们会找到有关 $\Delta{t}$ 的 $\Delta{s}$ 。那就是说

\[s+\Delta{s}=A(t+\Delta{t})^3+B(t+\Delta{t})+C=At^3+Bt+C+3At^2\Delta{t}+B\Delta{t}+3At(\Delta{t})^2+A(\Delta{t})^3，\]

由于

\[s=At^3+Bt+C，\]

我们求得

\[\Delta{s}=3At^2\Delta{t}+B\Delta{t}+3At(\Delta{t})^2+A(\Delta{t})^3\]

但是我们不想要 $\Delta{s}$ ，我们要的是 $\Delta{s}$ 除以 $\Delta{t}$ 。于是

\[\frac{\Delta{s}}{\Delta{t}}=3At^2+B+3At(\Delta{t})+A(\Delta{t})^2\]

随着 $\Delta{t}$ 趋近于零， $\Delta{s}/\Delta{t}$ 的极限是 $ds/dt$，等价于

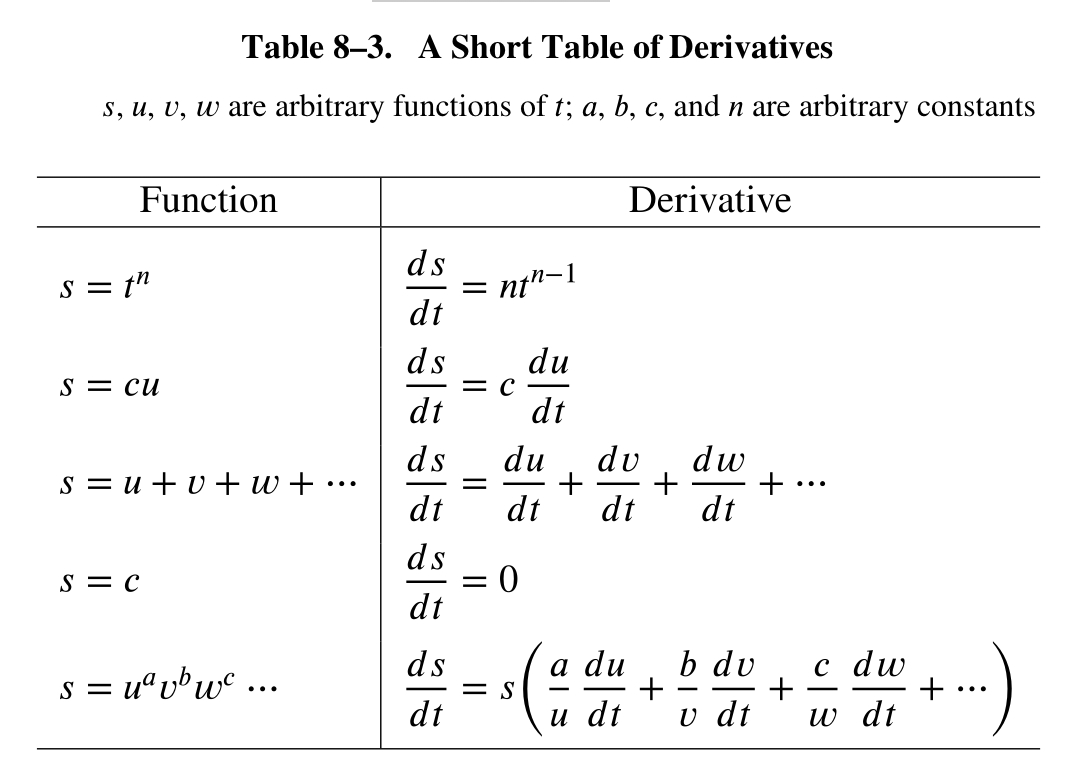
\[\frac{ds}{dt}=3At^2+B\]

这就是微积分的基础过程，微分函数。这个进程要比它看起来简单的多。我们观察到当这些展开包含 $\Delta{t}$ 的平方、立方或者更高的幂的元素时，它们可以被立即扔掉，因为当采用极限时它们会变为 0 。在做了一些练习之后，进程变得更加简单了，因为我们知道什么该被舍弃。微分各种类型的函数存有很多的规则或公式。这些可以被记住，也可以到表中查找。其中一些在表格 8-3 中被列出。