在超过 200 年的时间里，大家都以为由牛顿提出的运动等式正确地描述了自然，直到在这些定律中有一个错误首次被发现，修正它的方式也被发现。错误以及它的修正由爱因斯坦在 1905 年发现。

牛顿的第二定律，我们用等式表示为

\[F=d(mv)/dt\]

它默认 m 是一个常数，但是现在我们知道这是不对的，一个物体的质量随着速度增长。在爱因斯坦修正的公式中，m 的值为

eq-15-1

\[m=\frac{m_0}{\sqrt{1-v^2/c^2}}\]

其中“静止质量” $m_0$ 表示一个没有移动的物体的质量，c 是光速，大概是 $3 \times 10^5 km \cdot sec^{-1}$ ，或者大约 $186,000 mi \cdot sec^{-1}$ 。

对于那些想要学的刚刚好就能解决问题的人，这就是相对论的全部，它仅仅是在牛顿定律中的质量上引入了一个修正的因子。从公式本身可以很容易看出，在通常情况下，这个质量增长非常小。即使速度与人造卫星一样，卫星以 $5 mi/sec$ 围绕地球运动，那么 $v/c=5/186,000$ ：把它代入到公式中，对于质量的修正仅仅是二、三十亿分之一，根本无法观测到。实际上，通过观测大量的粒子，它们以几近光速运动，使得公式的正确性得到充分地验证。但是，这个效果通常会很小，让人不可思议的是理论的发现会先于实验的发现。经实验表明，以一个足够高的速度，效果是巨大的，但是它不是由这种方式发现的。让人觉得蛮有趣的是一条包含着如此细致改变（在它首次被发现的时候）的定律是如何通过实验与物理理论相结合的形式牵扯到光的。不少人对此做了贡献，最终的结论由爱因斯坦提出来。

事实上有两种爱因斯坦相对论。本章节涉及的是特殊相对论，在 1905 年提出。在 1915 年爱因斯坦公布了另一个理论，被称之为通用相对论。这条理论把特殊相对论扩展到了引力定律的范畴；我们在这儿不会讨论通用理论。

相对原理最初是由牛顿提及的，在他的运动定律的一个推论中：“在给定的一个空间中物体的运动都是相同的，无论该空间是静止，还是在以匀速沿着一条直线运动。”它的意思是，举个例子，如果一艘太空船以匀速在运动，在它里面做的所有实验以及产生的所有现象与它没有移动时一样，需要指出的是，没有人看向外面。这就是相对原理的含义。它是一个很简单的概念，唯一的问题是在一个运动系统里所做的实验是否与该系统静止时所做的一样。让我们首先检验一下牛顿定律在运动的系统中是否是一样的。

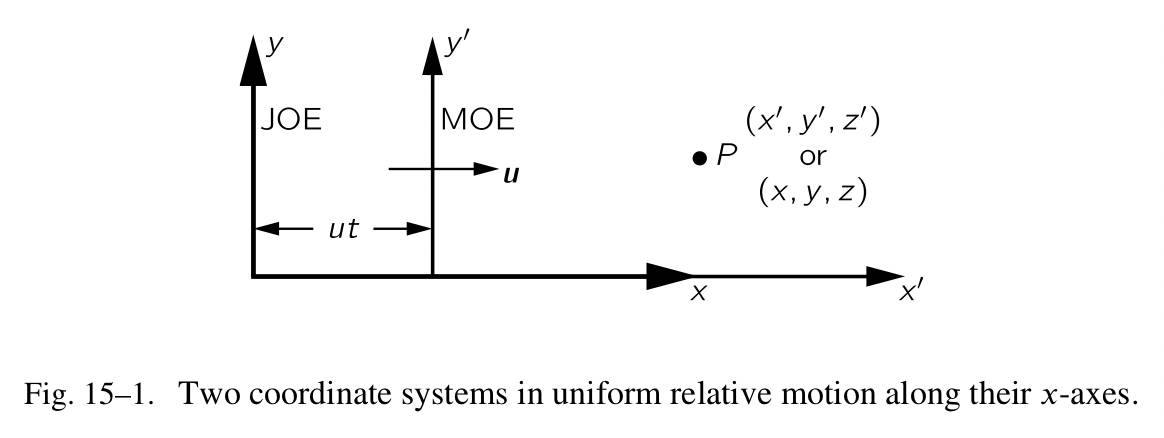
假设莫以匀速 u 沿着 x-方向在运动，他测量一个确定点的位置，如图 Fig.15-1 所示。 在他的坐标系中，他指定该点的”x-距离”为 $x’$ 。乔是静止的，他测量相同点的位置，在他的坐标系中，指定该点的 x-坐标为 x 。两个坐标系的关系在图中很清晰。在时间 t 之后，莫的原点移动了一段距离 ut ，如果两个坐标系原先是重合的，

eq-15-2

\[\begin{align*} x' &= x-ut, \\ y' &= y, \\ z' &= z, \\ t' &= t. \end{align*}\]

如果我们把上面代入到牛顿定律中，我们发现在运动系统中牛顿定律转换成了相同的定律；也就是说，在运动系统中的牛顿定律与静止系统中的是一样的。因此，我们不太可能通过做运动的实验来搞清楚系统是否在移动。

相对原理被应用到力学已经有很长的时间。很多人都使用过它，尤其是惠更斯，他获得了台球碰撞的原理，非常像我们在第 10 章运用它讨论动量守恒。在 19 世纪掀起了探索电、磁、光现象的浪潮。有很多人参与其中，最终促成了电磁场的麦克斯韦方程组的问世，它在一个统一的系统中描述了电、磁、光。然而，麦克斯韦方程组似乎并不符合相对原理。也就是说，如果我们通过代入等式 15.2来转换麦克斯韦方程组，它们不再保持相同；因此，在一个运动的太空船中的电和光的现象应该不同于在一个静止的船中的。可以利用这些光的现象去确定船的速率。尤其是，可以通过做出必要的光的或者电的测量来确定船的绝对速度。麦克斯韦方程组的结论之一是如果在场中有一处扰动，比如生成光，这些电磁波会以相同的速率 c ，或者 $186,000 mi/sec$ 均匀地沿着所有的方向运动。另一个结论是如果扰动的源正在移动，释放出的光会以相同的速率 c 穿越空间。这个可以类比于声音，声波的速率同样独立于源的运动。

这个独立性，在光的示例中，带来了一个有趣的问题：

假设我们正在驾驶一辆汽车，它的速率是 u，来自后方的光以速率 c 越过汽车。求导 15.2 中的第一个等式，得到

\[dx'/dt=dx/dt-u\]

它的意思是，按照伽利略变换，掠过的光的速率，正如我们在汽车里所测量的，应该不是 c ，而是 c-u 。举例说明，如果汽车以 $100,000 mi/sec$ 运动，光以 $186,000 mi/sec$ 运动，那么掠过汽车的光以 $86,000 mi/sec$ 运动。在任何情况下，通过测量掠过汽车的光的速率（如果伽利略变换对于光是正确的），可以确定汽车的速率。基于这个通用的观点做了不少的实验来确定地球的速度，它们全都失败了——根本给不了速度。我们会详细地讨论其中的一个实验，完整地展现做了什么，问题是什么；可以肯定的是某个物理等式出错了。是哪里呢？