在接下来的运动等式中我们会介绍另一个点子,它超过了速度的范畴,我们想知道,“速度是如何改变的?”在之前的章节中我们讨论过力在速度中发生变化。你也许曾经兴奋地听到过一辆汽车从静止到 60 英里一小时只需要 10 秒。通过这样的性能我们可以看到速率改变的有多快,但仅仅是均值。我们现在应该讨论的是下一级别的复杂性——速度改变的有多快。换句话说,速度在一秒钟改变多少英尺每秒,也就是,每秒,多少英尺每秒?我们之前得到的坠落物体的速度公式是 $v=32t$ ,它被记录在表格8-4 中,现在我们想搞清楚速度每秒改变多少,这个数值被称之为加速度。
加速度被定义为速度变化的时间比率。从之前的讨论中我们已经知道的足够多,可以把加速度写作导数 $dv/dt$ ,亦如速度是距离的导数。如果我们求导公式 $v=32t$ ,我们得到
\[a=\frac{dv}{dt}=32\]【我们可以利用之前问题的结果求导乘积 $32t$ ,因为我们发现 $Bt$ 的导数就是 $B$ (常数)。所以代入 $B=32$ ,我们可以立即得到 $32t$ 的导数是 32。】这表示一个坠落物体的速度每秒总是改变 32 英尺/秒。从表格8-4中,我们也看到速度每一秒增长 32 ft/sec。这是一个很简单的案例,加速度通常不是常数。加速度在这儿是常数的原因是在坠落物体上的作用力是常数,牛顿定律提到加速度与作用力成正比。
再举一个例子,让我们在一个已经解决的速度问题中寻求加速度。从
\[s=At^3+Bt+C\]开始,我们得到过 $v=ds/dt$ ,
\[v=3At^2+B\]因为加速度是速度相对于时间的导数,我们需要求导上面最后一个表达式。回忆一下规则,右边两项的导数等于单独项的导数之和。求导第一个二次项,不需要再走基本过程,因为我们求导过 $16t^2$ ;其结果是双倍数值系数,再把 $t^2$ 变成 $t$ ;让我们假设相同的事情会发生,你可以自行验证结果。 $3At^2$ 的导数会是 $6At$ 。接下来我们求导 $B$ ,一个常数项;根据之前表述的规则, $B$ 的导数是 0;因此该项不会留下。最终的结果是 $a=dv/dt=6At$
为了参考,我们写下两个有用的公式,它们可以通过积分获得。如果一个物体由静止开始且以一个恒定的加速度 $g$ 移动,它在任意时间 $t$ 的速度 $v$ 可以被给出
\[v=gt\]在相同时间跑的距离是
\[s=\frac{1}{2}gt^2\]各种数学符号被用来书写导数。因为速度是 $ds/dt$ ,加速度是速度的时间导数,我们也可写作
\[a=\frac{d}{dt}(\frac{ds}{dt})=\frac{d^2s}{dt^2}\]这是书写二阶导数的常见方式。
我们有另一个定律——速度是加速度的积分。这正好是 $a=dv/dt$ 的逆向;我们已经看到距离是速度的积分,所以我们可以通过两次积分加速度求得距离。
在之前的讨论中运动仅是一维的,而说到空间,我们可以做一个简短的讨论。考虑一个粒子 P ,它在三维中随意的移动。在章节伊始,我们通过观察汽车在各种时间相较其初始点的距离展开了一辆正在移动的汽车有关一维运动的讨论。然后我们讨论了速度,也就是距离伴随时间的改变,以及加速度,即速度的改变。我们可以类比地对待三维运动。首先在二维图解上阐述运动会更简单,然后扩展到三维。我们建立了一对坐标,互为直角,并且通过测量每两个坐标之间的距离来确定粒子在任意时刻的位置。因此每个位置给出一个 x-distance 和 y-distance,并且可以通过构建一个表格描述运动,在该表格中这些距离都被給作时间的函数。(扩展到三维仅需另一个坐标,垂直于前两个,即 z-distance。这些距离现在通过坐标平面确定,而不是线。)构建了一个 x- and y-distances 的表格,我们该如何确定速度?我们首先会找到在每个方向上的速度的部分。速度的水平部分,即 x-component,是 x-distance 相对于时间的导数,即
\[v_x=dx/dt\]相似地,速度的垂直部分,即 y-component,是
\[v_y=dy/dt\]在第三维,
\[v_z=dz/dt\]现在,给出速度的部分,我们该如何找到运动的真实路径上的速度?在二维案例中,考虑粒子的两个连续位置,相隔距离 $\Delta{s}$ 和时间 $t_2-t_1=\Delta{t}$ 。在时间 $\Delta{t}$ 内粒子水平移动一个距离 $\Delta{x}\approx{v_x\Delta{t}}$ ,垂直移动 $\Delta{y}\approx{v_y\Delta{t}}$ 。(符号 $\approx$ 读作“近似”。)真实移动地距离大约是
\[\Delta{s}\approx{\sqrt{(\Delta{x})^2+(\Delta{y})^2}}\]如图 Fig.8-3 所示。在间隔期间的近似速度可以通过除以 $\Delta{t}$ 获得,且让 $\Delta{t}$ 为 0,亦如章节伊始。然后我们得到速度
\[v=\frac{ds}{dt}=\sqrt{(dx/dt)^2+(dy/dt)^2}=\sqrt{v_x^2+v_y^2}\]对于三维,结果是
\[v=\sqrt{v_x^2+v_y^2+v_z^2}\]正如我们定义了速度,用相同的方式我们可以定义加速度:我们有一个加速度的 x-component $a_x$,它是 $v_x$ (速度的 x-component) 的导数(也就是, $a_x=d^2x/dt^2$ , $x$ 相对于 $t$ 的二阶导数),等等。

让我们考虑一个在平面上有关复合运动的不错实例。我们采纳的运动是一个球以恒定的速度 $u$ 水平移动,同时以一个恒定的加速度 $-g$ 向下坠落;这是什么运动?我们说 $dx/dt=v_x=u$ 。因为速度 $v_x$ 是常数,
\[x=ut\]因为向下的加速度 $-g$ 是常数,物体坠落的距离 $y$ 可以写作
\[y=-\frac{1}{2}gt^2\]它的路径曲线是什么,也就是, $x$ 和 $y$ 之间的关系是什么?我们可以从上面的等式移除 $t$ ,因为 $t=x/u$ 。替换之后,我们得到
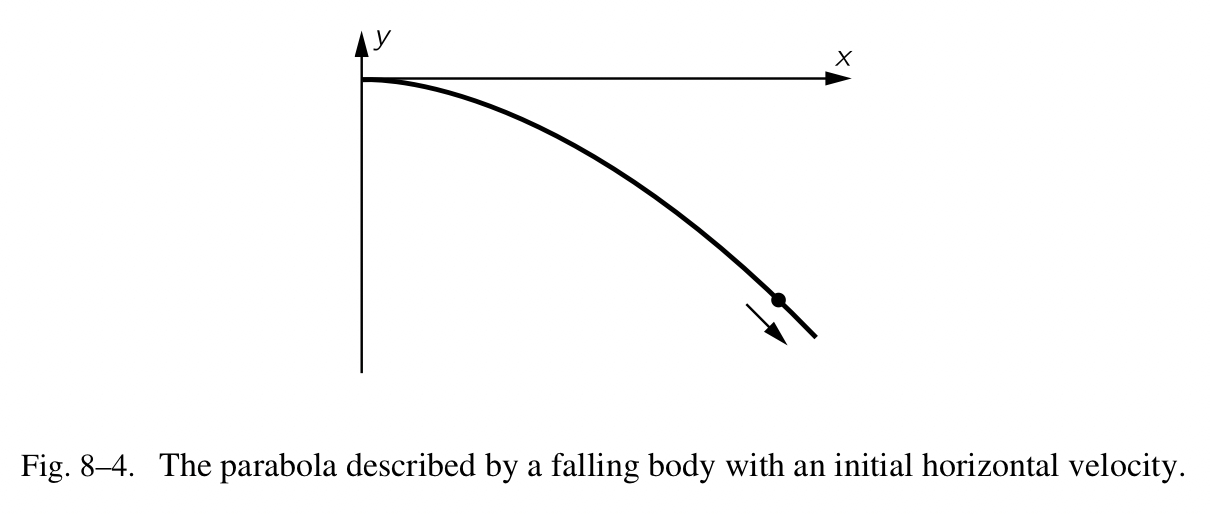
\[y=-\frac{g}{2u^2}x^2\]$y$ 和 $x$ 之间的关系也许可以作为正在移动的球体路径的等式。由这个公式绘制出来的曲线被称之为抛物线;以任意方向射出去的自由坠落的物体将会沿着抛物线运动,如图 Fig.8-4 所示。