现在我们要讨论剩下的基础作用力。我们称它们为基础的,因为从本质上它们的定律很简单。首先我们会讨论带电粒子的作用力。物体携带的电荷是由电子或者质子组成。如果任意两个物体带电,它们之间有一个作用力,如果电荷数分别是 $q_1$ 和 $q_2$ ,那么作用力与两电荷之间的距离的平方成反比, $F=(const)q_1q_2/r^2$ 。有点像引力定律,但是作用力是互斥的,符号(方向)相反。 $q_1$ 和 $q_2$ 要么是正的,要么是负的,如果 q 被正确地给定为正号或者负号,那么在公式的应用中作用力的方向会正确显示;作用力的方向位于电荷之间的连线上。公式的常数取决于作用力、电荷以及距离的单位。当前,电荷是库仑,距离是米,作用力是牛顿。为了正确地获得以牛顿为单位的作用力,常数(出于历史的原因被写作 $1/4\pi\epsilon_0$ )采纳的数值为:
\[\epsilon_0=8.854 \times 10^{-12} coul^2/newton\cdot{m^2}\]或者
\[1/4\pi\epsilon_0=8.99 \times 10^9 N\cdot{m^2}/coul^2\]因此静电的作用力定律是:
\[\boldsymbol{F}=q_1q_2\boldsymbol{r}/4\pi\epsilon_0r^3\]最为重要的是在一个单独电子上的电荷,它是 $1.60\times{10^{-19}}$ 库仑。对于基础粒子的带电的作用力,而非大量的电荷,人们更喜欢的是 $(q_{el})^2/4\pi\epsilon_0$ 这个组合,其中 $q_{el}$ 被定义为一个电子上的电荷。该组合会频繁地出现,为了简化计算,它被定义为符号 $e^2$ ;在 MKS 系统中,它的数值是 $(1.52\times{10^{-14}})^2$ 。这样写常数的好处是,两个电子之间的作用力(以牛顿为单位)可以简化为 $e^2/r^2$ ,其中 r 是米,无需列出单独的常数。带电的作用力要比这个简单的公式复杂许多,因为该公式给出的是两个物体之间的作用力,这两个物体处于静止的状态。我们马上会给出更通用的。
在分析更加基础的粒子中(不是摩擦力那种,而是带电的作用力和引力),一个有趣且重要的概念被开发出来。因为起初作用力要比平方反比定律复杂得多,这些定律只有在交互的物体是静止时才是有效的,我们需要一个升级的方法处理非常复杂的作用力,当物体以一种复杂的方式开始移动。对于这种作用力的分析,“场”的概念非常有用。为了阐述这个观点,假设我们有两个电荷 $q_1$ 和 $q_2$ ,它们分别位于 P 点和 R 点。电荷之间的作用力如下:
\[\boldsymbol{F}=q_1q_2\boldsymbol{r}/4\pi\epsilon_0r^3\]用场的概念去分析这个作用力,在 P 处的电荷 $q_1$ 在 R 处产生了一个“状态”,当电荷 $q_2$ 被放在 R 处,它“感受到了”作用力。这样说或许有些奇怪,在 R 处 $q_2$ 上的作用力可以被写成两个部分。 $q_2$ 乘以数值 $\boldsymbol{E}$ ,不管 $q_2$ 是否在那儿, $\boldsymbol{E}$ 总是在的(我们确保所有其他的粒子都在自己的位置上)。 $\boldsymbol{E}$ 是由 $q_1$ 产生的“状态”, $\boldsymbol{F}$ 是 $q_2$ 对 $\boldsymbol{E}$ 的响应。 $\boldsymbol{E}$ 被称之为电场,它是一个向量。在 R 处的电场的公式是电荷 $q_1$ 乘以常数 $1/4\pi\epsilon_0$ 除以 $r^2$ (r 是 P 到 R 的距离),它作用在半径向量的方向上(半径向量 r 除以它的自身长度)。 $\boldsymbol{E}$ 的表达式写作:
eq-12-4
\[\boldsymbol{E}=q_1\boldsymbol{r}/4\pi\epsilon_0r^3\]进而
eq-12-5
\[\boldsymbol{F}=q_2\boldsymbol{E}\]显示出作用力、场以及场中的电荷。所有的这些重点是啥?重点是把分析拆分成了两部。第一部是说某种东西生成了一个场。第二部是说场作用在某种东西上。像这种拆分允许我们单独地查看各自的部分,它在许多情形中简化了计算。如果出现了很多电荷,我们首先计算由所有的电荷在 R 处产生的电场,然后,知道了在 R 处的电荷,我们就能获得在它上面的作用力。
在引力的示例中,我们可以做一样的事儿。其中 $\boldsymbol{F}=-Gm_1m_2\boldsymbol{r}/r^3$ ,我们可以做一个类比分析:在引力场中的一个物体上的作用力是该物体的质量乘以力场 $\boldsymbol{C}$ 。 $m_2$ 上的作用力是质量 $m_2$ 乘以由 $m_1$ 产生的力场 $\boldsymbol{C}$ ;也就是, $\boldsymbol{F}=m_2\boldsymbol{C}$ 。由 $m_1$ 产生的力场 $\boldsymbol{C}$ 是 $\boldsymbol{C}=-Gm_1\boldsymbol{r}/r^3$ ,它是半径朝向,如同带电的示例。
不管起初它看起来如何,这样的拆分非常重要。如果作用力的定律很简单,仅仅是用另一种方式书写同样的事情,才是毫无价值,实际上作用力的定律非常复杂,它表明场有一个实体,几乎与创造它的东西无关。某人可以摇晃一个电荷,生成一个效果,一个场,在一段距离;如果有人停下移动的电荷,场会记录所有的过去,因为两个粒子之间的交互不是瞬时的。它需要某种方式记住之前发生了什么。如果某个电荷上的作用力取决于昨天另一个电荷的位置,我们需要某个功能记录昨天发生了什么,这是场的特性。所以当作用力变得更加复杂,场会变得越来越真实,这种科技越来越不可能由人工操作。
用场分析作用力,我们需要两种与场相关的定律。第一个是关于场的响应,它给出了运动等式。比如,一个质量对一个引力场的响应定律是作用力等于质量乘以引力场;或者,在物体上有一个电荷,电荷对电场的响应等于电荷乘以电场。自然分析的第二部分是公式化这些定律,确定场的强度以及它是如何产生的。这些定律有时被叫做场方程。我们会在合适的时间学更多,现在写下一些。
首先,最为引人瞩目的事实(它可以很容易被理解)是由一些源产生的全部的电场是各个电场的向量之和,由第一个源产生的、由第二个源,等等。也就是说,如果我们有很多电荷,制造了一个场,如果其中之一制造了场 $\boldsymbol{E}_1$ ,另一个制造了场 $\boldsymbol{E}_2$ ,等等,那么我们仅需把这些向量相加就能得到全部的场。这个原理被表示为:
eq-12-6
\[\boldsymbol{E}=\boldsymbol{E}_1+\boldsymbol{E}_2+\boldsymbol{E}_3+ \cdots\]或则
eq-12-7
\[\boldsymbol{E}=\sum_{i}\frac{q_i\boldsymbol{r}_i}{4\pi\epsilon_0r_i^3}\]同样的方法可以应用到引力上吗?质量 $m_1$ 和 $m_2$ 之间的作用力由牛顿表示为 $\boldsymbol{F}=-Gm_1m_2\boldsymbol{r}/r^3$ 。但是根据场的概念,我们或许会说 $m_1$ 在其周围创造了一个场 $\boldsymbol{C}$ ,在 $m_2$ 上的作用力是:
eq-12-8
\[\boldsymbol{F}=m_2\boldsymbol{C}\]完全类比带电的情况:
eq-12-9
\[\boldsymbol{C}_i=-Gm_i\boldsymbol{r}_i/r^3\]由若干质量产生的引力场是:
eq-12-10
\[\boldsymbol{C}=\boldsymbol{C}_1+\boldsymbol{C}_2+\boldsymbol{C}_3+\cdots\]在第九章,处理行星运动的问题,本质上使用的是这个定律。我们简单地把所有的作用力向量相加,就能得到一个行星上的全部作用力。如果我们除以行星的质量,就得到 Eq.12.10。
等式 12.6和 12.10 反应出场的叠加原理。该原理表明由所有源导致的全部场是每个源导致的场之和。迄今为止,对于电,这是一条绝对有保障的定律,即使作用力定律由于电荷的运动变得复杂也没错。这儿有明显的冲突,但是经过仔细地分析,我们发现那是由于忽略了电荷的移动造成的。虽然叠加原理完全适用带电的作用力,它并不适用引力如果力场太强的话,牛顿等式 12.10 是近似的,根据爱因斯坦的引力理论。
与带电的作用力紧密相关的是另一种,叫做磁力,它也可以用场来分析。带电的作用力与磁力之间的某些非量化关系可以由一个阴极射线管的实验(fig.12-3)表述。在管子的一端有一处源释放出电子。在里面有一处装置用于加速电子,把它们中的一些以一束射线打到另一端的荧光屏上。一个光斑出现在屏幕中心,这使得我们可以追踪电子的路径。在抵达屏幕的路上,电子束通过一段狭窄的空间,那是一对水平放置的金属片。电压可以加到金属片上,所以任一片儿都能被弄成负的。当开启电压,金属片之间存在电场。
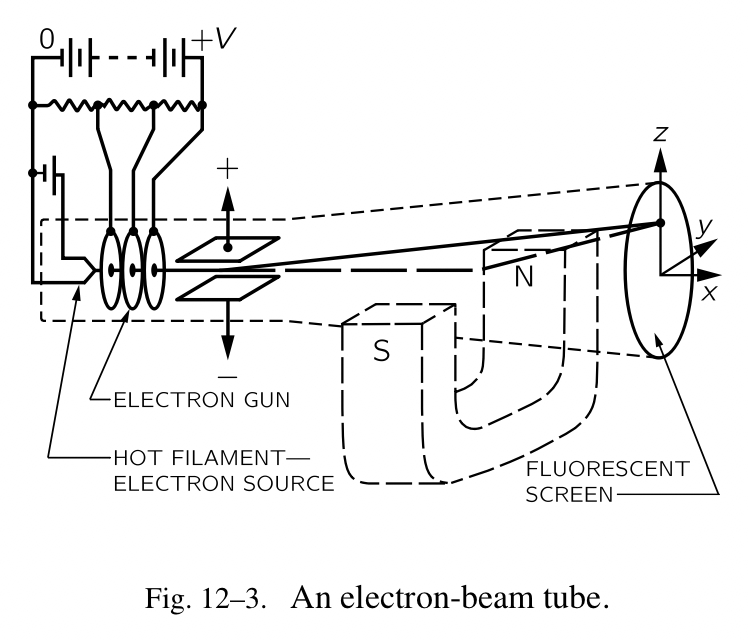
实验的第一个部分是把一个负电压加在下面的金属片上,也就是额外的电子被放置在下面的金属片上。因为电荷互斥,屏幕上的光斑立马上扬(我们可以换一种方式说,电子“感受到”场,通过向上改变来回应)。接下来我们反转电压,把上面的金属片弄成负的。屏幕上的光斑现在跳到了下面,表明电子束被它上面的金属片的电子排斥(我们也可以说,电子为了“响应”场,变了方向)。
实验的第二部分是切断金属片上的电压,测试电子束上的磁场效果。可以使用马蹄型磁铁,它的磁极刚好横跨管子。如果我们把磁铁放在管子下面,其方位如同字母 U,磁极朝上,部分管子介于两极中。随着磁铁从下面靠近管子,我们注意到光斑向上变化。似乎是磁铁排斥了电子束。然而,并非如此,如果我们上下翻转磁铁,不改变它的磁极,从上面靠近管子,光斑依然向上移动,所以电子束没有被排斥,这次似乎是被吸引。现在我们重新开始,恢复磁铁到初始方位,把它放到管子下面。光斑仍然向上变化,现在我们绕着垂直轴把磁铁旋转180度,它依然是 U 型,但是反转了磁极。快看,光斑跳到了下面,纵然是上下翻转磁铁,再从上靠近。
为了理解这个怪异的行为,我们得有一个全新的融合的作用力。我们这样解释:从一个磁极到另一个磁极存在一个磁场。这个磁场有一个方向,总是从一个磁极(我们可以标记)指向另一个。上下翻转磁铁不会改变磁场的方向,但是反转磁极会改变。比如,电子的速度是在水平的 x-方向上,磁场也是水平的,但是在 y-方向上,在移动的电子上的磁力在 z-方向上,朝上或者朝下,取决于磁场是在正的 y-方向上还是在负的 y-方向上。
虽然我们现在不会给出正确的作用力定律,介于随机移动的电荷之间,一个相对于另一个,因为它太复杂了,我们会给出部分:完整的作用力定律,如果场是已知的。一个带电物体上的作用力取决于它的运动;当物体在一处静止,存在某个作用力,它与电荷成正比,其系数被我们叫做电场。当物体在移动,作用力或许会不同,准确来讲,这“片儿”新的作用力完全依赖于线性速度,但是垂直于 $\boldsymbol{v}$ 和另一个向量,我们称其为磁力感应 $\boldsymbol{B}$ 。如果电场 $\boldsymbol{E}$ 和磁场 $\boldsymbol{B}$ 的部分分别是 $(E_x,E_y,E_z)$ 、 $(B_x,B_y,B_z)$ ,如果速度 $\boldsymbol{v}$ 的部分是 $(v_x,v_y,v_z)$ ,那么在一个移动电荷上的全部的带电的作用力和磁力拥有部分:
eq-12-11
\[F_x=q(E_x+v_yB_z-v_zB_y)\] \[F_y=q(E_y+v_zB_x-v_xB_z)\] \[F_z=q(E_z+v_xB_y-v_yB_x)\]如果仅有的磁场部分是 $B_y$ ,仅有的速度部分是 $v_x$ ,那么剩下的磁力只会在 z-方向上,垂直于 $\boldsymbol{B}$ 和 $\boldsymbol{v}$ 。