在自然中存在着确定的作用力，例如，引力，它有一个非常瞩目的特征，我们称之为“守旧”（不包含政治观点，它也是“疯狂单词”中的一个）。如果我们要计算在一个力的作用下一个物体沿着某个弯曲的路径从一个点移动到另一点做了多少功，在通常情况下功取决于曲线，但是在特殊的例子中并不是。如果它不取决于曲线，我们说该作用力是一个守恒的力。换言之，如果作用力乘以位置 1 到位置 2 的距离（如图 14-2 所示）的积分由沿着曲线 A 计算所得，然后沿着曲线 B，我们得到相同数量的焦耳，如果对于每一条曲线上的这个结对的点都是对的，如果相同的结论总是奏效，不管我们采用哪个结对的点，那么我们可以说该作用力是守恒的。在这样的情形中，由 1 到 2 的功的积分可以以一种简单的方式估算，我们可以为此给出一个公式。通常这并不容易，因为我们还是得明确曲线，但是当我们看到一个示例，其中的功不取决于曲线，当然，它只取决于 1 和 2 的位置。

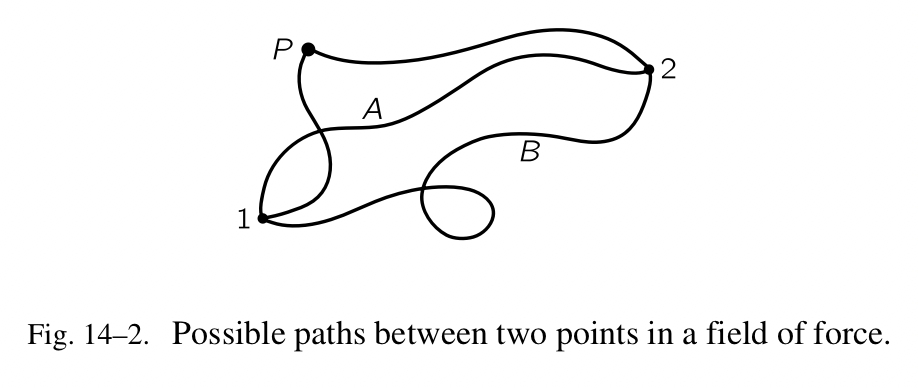
为了论述这个观点，会做下面的。我们取一个“标准”点 P，在任意的一个位置（如图 Fig.14-2 所示）。那么，由 1 到 2 所做的功，我们想要计算的，可以这样，由 1 到 p 所做的功加上由 p 到 2 所做的功，因为作用力是恒定的且功不取决于曲线。现在，由位置 P 到空间中的一个特定位置所做的功是在空间中该位置的一个函数。当然，它也取决于 P，但是为了分析，让我们把这个随机的点 P 固定下来。如果这样做的话，由点 P 到点 2 所做的功是最终位置 2 的某个函数。它取决于 2 的位置；如果我们移到其他位置，会得到不同的结果。

我们应该称该位置的函数为 $-U(x, y, z)$ ，当我们想要参照某个特定的点 2，它的坐标是 $(x_2, y_2, z_2)$ ，我们可以写作 $U(2)$ ，它是 $U(x_2, y_2, z_2)$ 的简写。由点 1 到点 2 所做的功也可以被写作是沿着积分的另一个方向，反转所有的 $d\boldsymbol{s}$ 。也就是，由 1 到 P 所做的功是负的由 P 到 1 所做的功：

\[\int_1^P\boldsymbol{F}\cdot d\boldsymbol{s}=\int_P^1\boldsymbol{F}\cdot (-d\boldsymbol{s})=-\int_P^1\boldsymbol{F}\cdot d\boldsymbol{s}\]

因此由 P 到 1 所做的功是 $-U(1)$ ，由 P 到 2 所做的功是 $-U(2)$ 。那么由 1 到 2 的积分等于 $-U(2)$ 加上 $-U(1)$ 的反方向，或者 $+U(1)-U(2)$ ：

eq-14-1

\[U(1)=-\int_P^1\boldsymbol{F}\cdot d\boldsymbol{s},\quad U(2)=-\int_P^2\boldsymbol{F}\cdot d\boldsymbol{s}\] \[\int_1^2\boldsymbol{F}\cdot d\boldsymbol{s}=U(1)-U(2)\]

数值 $U(1)-U(2)$ 被称为势能的变化，我们把 $U$ 称为势能。我们说当物体位于位置 1 时，它有势能 $U(1)$，在位置 2 时，它有势能 $U(2)$ 。如果它位于位置 P，它有零势能。如果我们采用其他的任意点，比如 Q，不是 P，它会证明势能的改变仅仅是增加一个常数（我们把它留给你去论证）。因为能量守恒仅仅取决于变化，是否在势能上增加一个常数无关紧要。因此点 P 是任意的。

现在，我们有了下面两个论点：（1）由一个作用力所做的功等于粒子的动能变化，但是（2）数学地表达，对于一个守恒的作用力，做的功是负的一个函数 $U$ 的变化，我们称 $U$ 为势能。由此得到的结论是，如果仅有守恒的作用力作用，动能 $T$ 加上势能 $U$ 保持恒定：

eq-14-2

\[T+U=constant\]

现在让我们讨论与势能的公式有关的一些示例。如果我们有一个引力场，它是统一的，如果我们到达的高度不及地球的半径，那么作用力是一个恒定的、垂直的力，它做的功就是作用力乘以垂直距离。因此，

eq-14-3

\[U(z)=mgz\]

对应零势能的点 P 可以是在 $z=0$ 的平面中的任意的点。我们也可以说势能是 $mg(z-6)$ ，如果我们想的话——所有的结果，当然，在我们的分析中是一样的，除了在 $z=0$ 处的势能的值是 $-6mg$ 。它没有任何区别，因为仅有的不同在于势能的计数。

把一个线性弹簧由一个平衡点压缩一个距离 $x$ 所需要的能量是：

eq-14-4

\[U(x)=\frac{1}{2}kx^2\]

零势能是在点 $x=0$ 处，弹簧的平衡位置。我们可以添加任意的常数。

对于质量点 $M$ 和 $m$ ，相距一个距离 $r$ ，引力势能是：

eq-14-5

\[U(r)=-GMm/r\]

常数在这儿被敲定，因此在无限处势能是零。相同的公式适用于电荷，因为它有相同的定律：

eq-14-6

\[U(r)=q_1q_2/4\pi\epsilon_0r\]

现在让我们使用一下这些公式，来看看是否理解它。问题：为了让一个火箭离开地球我们需要以多快的速度发射它？答案：动能加上势能一定是一个常数；当它“离开”时，它将相距百万英里，如果它只是刚好离开，我们或许认为它在那儿是以零速移动，几乎未动。让 $a$ 为地球的半径， $M$ 是它的质量。动能加上势能被初始化为 $\frac{1}{2}mv^2-GmM/a$ 。在运动的结束，两个能量肯定相等。在运动的结束，动能为零，是因为它被认为是几乎以零速在移动，势能是 $GmM$ 除以无限，为零。在一边，所有的一切都是零，这告诉我们速度的平方一定是 $2GM/a$ 。但是我们称 $GM/a^2$ 是引力的加速度， $g$ 。因此

\[v^2=2ga\]

让一个卫星环绕地球需要多快？我们很早之前就解决了， $v^2=GM/a$ 。因此为了离开地球，我们需要 $\sqrt{2}$ 倍的速度——环绕地球表面所需的。换言之，我们需要两倍的能量（因为能量随着速度的平方增长）离开地球，相比环绕着它运动。因此之前所做的第一件事儿是让一个卫星环绕地球，需要 5 英里每秒的速度。接下来是发送卫星离开地球；这需要两倍的能量，或者大约 7 英里每秒的速度。

现在，让我们继续讨论势能的特性，涉及两个分子的交互，或者两个原子，比如两个氧原子。当它们离得很远，作用力是一种吸引力，它与距离的七次幂成反比，当它们离得很近，作用力是很大的互斥力。如果我们通过计算七次幂的反比的积分，求得做的功，那么势能 $U$ 是一个介于两个氧原子之间的半径的距离函数，它与距离的六次幂成反比，对于巨大的距离。

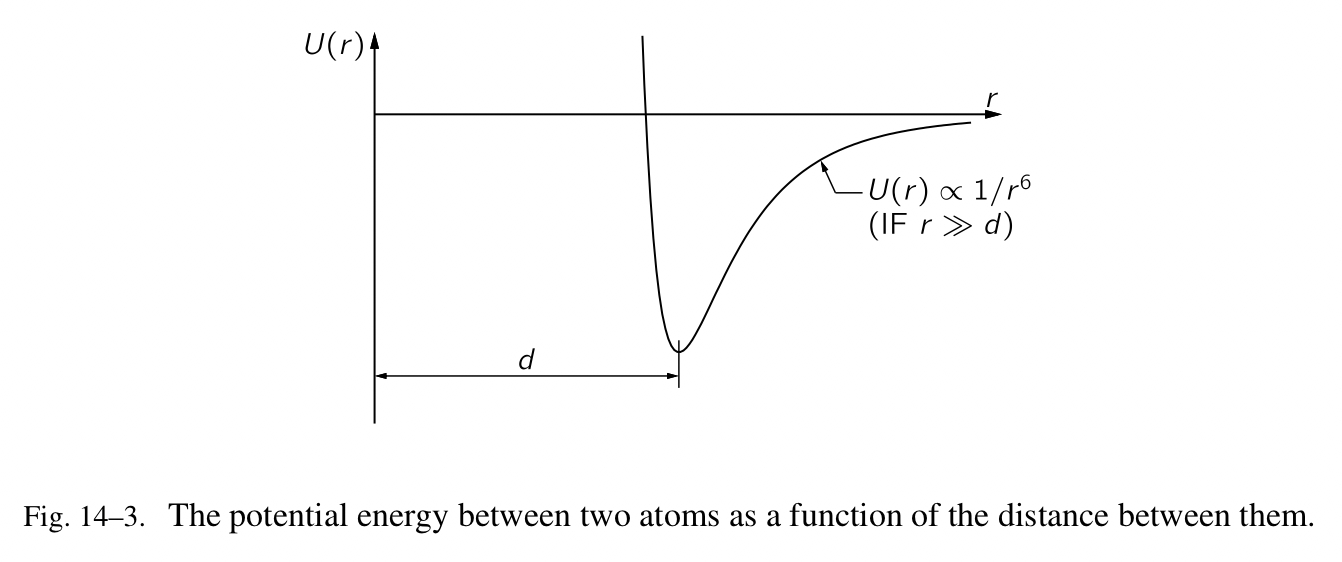
如果我们如图 Fig.14-3 所示绘制势能 $U(r)$ 的曲线，我们看到在较远的 $r$ 处，与六次幂成反比，但是如果我们非常靠近点 $d$ ，那儿有最小的势能。在 $r=d$ 处的最小的势能表示：如果我们在 $d$ 处启动，移动一个非常小的距离，所做的功，也就是势能的变化，几近于零，因为在曲线的底部势能几乎没有变化。因此在这个点上没有作用力，所以它是平衡点。另一种认为它是平衡点的方式是沿着任意方向由 $d$ 离开需要做功。当两个氧原子安静下来，没有更多的能量被释放，从它们之间的作用力中，它们处于最低的能量状态，它们位于这段儿 $d$ 处。这就是一个氧原子受冷时的样子。当我们加热，原子摇晃且移得更远，我们实际上分离了它们，但是这样做需要一定数量的功或能量，它是 $r=d$ 与 $r=\infty$ 之间的势能差。当我们把原子推得非常地近，能量迅速飙升，因为它们互相排斥。

我们这样说的原因是，作用力的概念不太适合量子力学，在那儿，能量的概念最为普遍。我们发现，虽然作用力和速度“溶解”、消逝，当我们考虑更高阶的作用力，在原子核物质之间以及在分子之间，等等，但是能量的概念保留了下来。因此我们在量子力学的书中会发现势能的曲线，但是几乎看不到两个分子之间的作用力的曲线，这是因为那时做分析的人考虑的是能量，而不是作用力。

现在我们留意到，如果几个守恒的作用力在同一时间被作用到一个物体上，那么这个物体的势能是来自每一个分离的作用力的势能的和。这是一个我们之前提及的相同论述，因为如果作用力可以被表示为作用力的一个向量之和，那么由全部的作用力所做的功是由部分的作用力所做的功的和，因此它可以被当作是每一个单独部分的势能变化去分析。全部的势能是所有小片儿的和。

我们可以把它推广到一个系统的示例，包含很多彼此交互的物体，像是木星、土星、天王星，或者，氧原子、氮原子、碳原子，等等…它们在力的作用下以结对的形式相互作用，这里的作用力都是守恒的。在这些情形中，整个系统的动能是所有具体的原子或者行星或者其他的动能的和，系统的势能是遍历所有的粒子对，一个单独结对的相互作用的势能的和，就好像其他的不在那儿。（对于分子的作用力是不正确的，公式在某种程度上更加复杂；对于牛顿的引力显然是正确的，对于分子的作用力近似正确。对于分子的作用力，这儿有一个势能，它有时是一个更加复杂的有关原子位置的函数，而不是简单地把来自结对的元素相加求和。）在特殊的引力示例中，势能是遍历所有的结对 $i$ 和 $j$ ， $-Gm_im_j/r_{ij}$ 的和，就像等式13.14 那样。等式13.14采用数学的方式作出了下面的论述：全部的动能加上全部的势能不会随着时间改变。就像各种行星齿轮，它们旋转、环绕，等等，如果我们计算全部的动能和全部的势能，我们发现整体保持恒定。