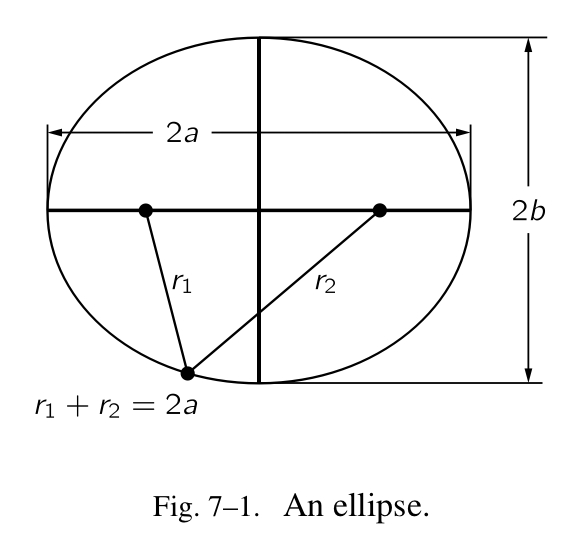
首先，开普勒发现每一个行星都围绕着太阳运动，它运行的轨道是一个椭圆，太阳在其中的一个焦点上。行星的轨道不仅仅是一个椭圆，而是一个非常特别和精确的环形，我们可以通过在白纸上任意的两个固定点上放置两个图钉，再加上一圈线（线圈应该能够覆盖两个固定点）和一支笔，模拟出该形状；更具数学的表达是，它是所有的交汇点——其与两个固定点的距离之和是一个常数。或者，你可以把它当作是缩减的圆。

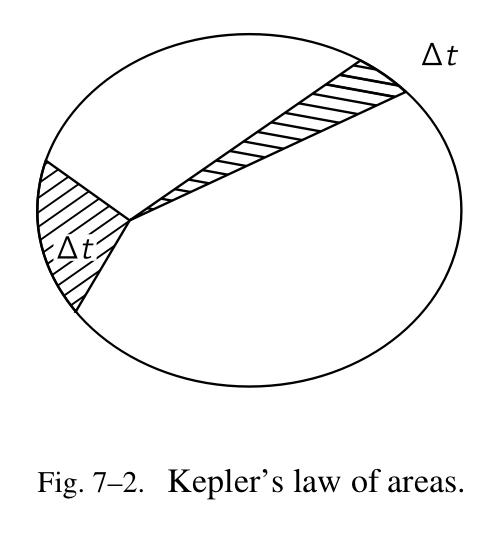
开普勒观察到的第二个结果是行星不是以相同的速度围绕太阳运行，而是距离太阳越近速度越快，距离太阳越远速度越慢，精确地讲，如果一个行星在两个连续的时间点被观测，中间间隔一周，那么对于每一个观测点，位置向量被画出指向行星。行星在一周里运行的轨迹，加上两个位置向量，形成了一个确定的区域，如图 Fig-7-2 的阴影所示。如果两个相似的观察相隔一周，在距离太阳更远的轨道的那一部分（行星会运行的更慢），形成的区域的面积与上一次完全相等。所以根据第二定律，轨道的半径以行星的速度“扫描出来”的面积在相同的时间段里都是相等的。

最终，开普勒在更晚的时候发现了第三定律，该定律相比较其他两个是一个不同的类型，因为它面对的不仅仅是一个单独的行星，而是一个行星相对于另外一个。当任意两个行星的环绕的周期和轨道的大小被拿来比较的话，周期与轨道大小的 $3/2$ 的幂成正比。在这个描述里，周期是一个行星完整地绕着轨道运行一圈所花费的时间，大小测量的是椭圆轨道最大直径的长度，技术上被称之为主轴。简单来讲，如果行星是围绕环形做运动，那么围绕环形运动所要花的时间将与直径（或半径）的 $3/2$ 的幂成正比。因此，我们可以总结一下开普勒的三个定律：

1. 每一个行星都是围绕太阳在一个椭圆的轨道上运行，太阳在轨道的一个焦点上。
2. 从太阳指向行星的位置向量所扫描出来的面积在相同的时间间隔里面相等。
3. 任意两个行星的周期的平方与它们各自轨道的半主轴的立方成正比： $T \propto{a^{3/2}}$