出于他对运动理论更好的理解，牛顿意识到太阳应该是裁定者或者说是力的策划者，它控制了行星的运动。牛顿证明了这个事实（很快，也许我们也可以证明它），在相同的时间段里扫描出相等的面积是一个明显的信号，它论述了所有的偏离运动都是与半径相关的——面积定律是这个观点的直接产物，所有的力都朝向太阳。

接下来，通过分析开普勒的第三定律，它或许揭示了行星越远，力越弱。如果对距离太阳不同位置的两个行星进行比较，分析说明力与各自距离的平方成反比。结合这两个定律，牛顿总结出一定有一个力，与距离的平方成反比，指向两个物体之间的连线。

经过仔细地思考，牛顿概括出这个关系应该可以更加通用化，相比于太阳维系行星。众所周知，木星拥有围绕它运动的卫星，就像月亮之于地球，牛顿可以确定每一个行星都借由一个力维系着它的卫星。他已经知道了维系我们在地球上的力是什么，所以他提出这是一个无所不在的力——一切的事物都拉拽着一切其他的事物。

下一个问题是地球对于其上人们的拉力是否与其对月亮的拉力“一样”，例如，与距离的平方成反比。如果一个地球表面的物体坠落了 16 英尺，在它从静止的状态释放之后的头一秒，在相同的时间段里月亮坠落了多远？我们也许会说月亮根本没有坠落。不过，假设没有力作用在月亮上的话，它应该走的直线，然而它做的是环形运动，所以相较于它的初始位置，它确实坠落了。我们可以通过月亮轨道的半径（大约是 240,000 英里）和它绕地球一圈所花费的时间（大约是 29 天）计算出，在一秒中它在轨道上走了多远，然后再计算出在一秒中，它坠落了有多少。这个距离大概是 $1/20$ 英寸。它很好的契合了平方反比定律，因为地球的半径是 4,000 英里，如果距离地球中心 4,000 英里的某个物体在一秒中坠落了 16 英尺，某个物体的位置是 240,000 英里，或者 60 倍那么远，应该会坠落 16 英尺的 $1/3600$，换算下来，也大约是 $1/20$ 英寸。牛顿希望通过相似地计算验证引力的理论，他非常仔细，发现结果出入很大，他认为该理论与事实不符，所以就没有发表。六年以后，一个关于地球大小的新的测量被发现，它表明天文学家曾经使用了错误的值计算月亮的距离。牛顿听说之后，再次进行了计算，得到了一致的答案。

fig-7-3

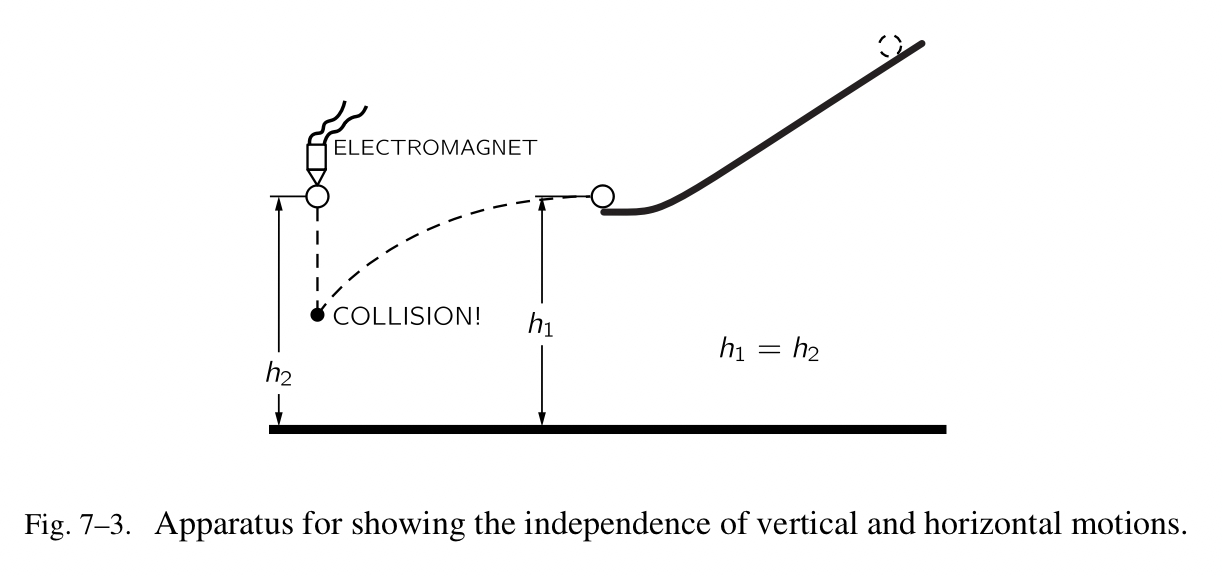
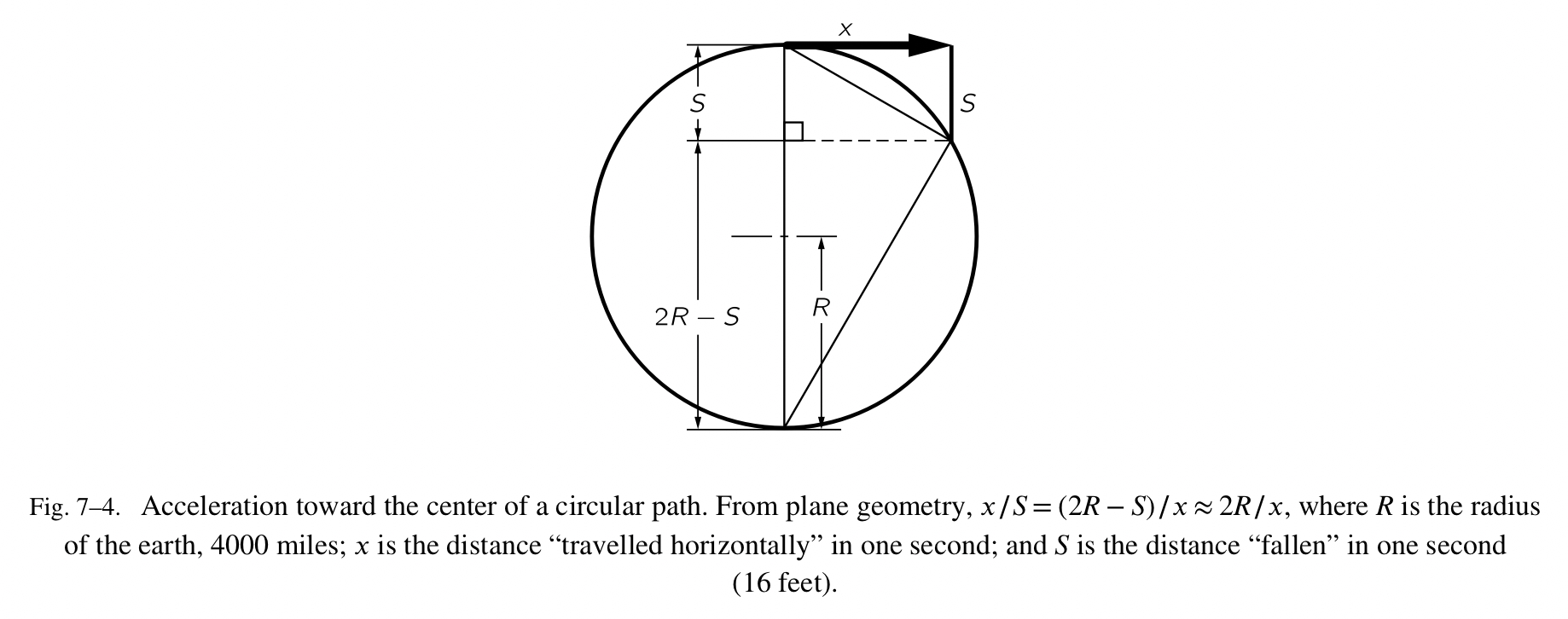
月亮坠落的这个观点存有某些疑惑，因为，正如你所见，它并没有靠的更近。这个点子非常的有趣，值得进一步地阐释：在该场景中，月亮是相较于切线坠落（假设没有力的作用，月亮本应保持着直线运动）。让我们举一个地球表面的例子。一个物体在地球表面附近被释放，它将在头一秒坠落 16 英尺。一个沿着水平方向射出的物体也会坠落 16 英尺；即使它是水平运动，它仍然会在相同的时间里坠落相同的 16 英尺。图 7-3 显示的就是这样的一个设备。一个水平的轨道引导了一个球行径了一段距离。在相同的高度上，一个球垂直坠落，那里被安置了一个电子开关，这样的话，在第一个球离开轨道的同时，第二个球被释放出来。我们可以亲眼目睹，它们会相撞在一起。一个像子弹的物体，水平射出，也许在一秒里会走的很远——大概 2,000 英尺——但是它仍然会坠落 16 英尺，相较于水平方向。如果我们射出来的子弹越来越快，会发生什么？不要忘记地球的表面是曲形的。如果我们射的足够的快，当它坠落 16 英尺的时候，它也许正好位于之前它距离地面的相同的高度。这怎么可能呢？它仍然在坠落，但是地球掰弯了它，，使得它“绕着”地球坠落。问题来了，它在一秒里要跑多远，才能让地球位于水平方向下方 16 英尺的位置？在图 7-4 中，我们看到地球的半径是 4,000 英里和它的切线，也就是直线路径——如果没有力的左右，子弹所行径的。现在，如果我们使用几何学中一些美妙的定理，其中指出我们的切线是介于由一个相等的弦所分割的直径的两个部分之间的 mean proportional （ $x/S=(2R-S)\approx{2R/x}$ ）。我们看到行径的水平距离是介于坠落的 16 英尺与 8,000 英里的地球直径之间的 mean proportional。 $(16/5280)\times{8000}$ 的平方根很接近 5 英里。因此我们看到如果子弹以每秒 5 英里的速率移动，它将会持续性地朝着地球坠落，以每秒 16 英尺的相同速率，但是它不会再靠的更近，是因为地球始终让它保持着环形运动。因此加加林先生就是这样维持着自身在太空中以大概每秒 5 英里的速率绕着地球行径了 25,000 英里。（他可能会花费更长一点的时间，因为他位置稍高。）

我们得到的比我们付出的更多，这就是任意一个新的定理的伟大发现的有用之处。现在，牛顿使用了开普勒的第二和第三定律，推导出引力的定理。那么，他预测了什么？首先，他对于月亮运动的分析是一个预测，因为它结合了地球表面物体的坠落和月亮的运动。其次，有个问题，轨道是椭圆的吗？我们在稍后的章节应该可以精确地计算运动，事实上能够证明它是一个椭圆，所以不需要再额外解释开普勒第一定律。牛顿做出了他的首个无与伦比的预测。

引力定理阐释了之前无法理解的许多现象。举个例子，在地球上月亮的拉力引发了潮汐，一个特定时间的神秘现象。月亮拉升了位于其下的水，导致了潮汐——之前人们是这样认为的，但是他们没有牛顿那么聪明，他们认为在一天之中仅会发生一次潮汐。是因为月亮的拉力，导致了高潮和低潮，再加上地球自身的旋转，它导致了每 24 个小时在同一个位置上潮汐出现了起落。实际上潮汐会每 12 个小时出现起落。在学校里也许有人会澄清高潮会出现在地球另外一边的原因是月亮把地球拉离了水！这些理论都是错误的。它实际上是这样工作的：月亮对于地球和水的拉力在中心位置“被平衡了“。但是距离月亮更近的水较于平均被拉拽的更多，距离它越远的水较于平均被拉拽的更少。进一步地说，水可以流动，但是地球不能。真实的图像是这两则事物的融合。

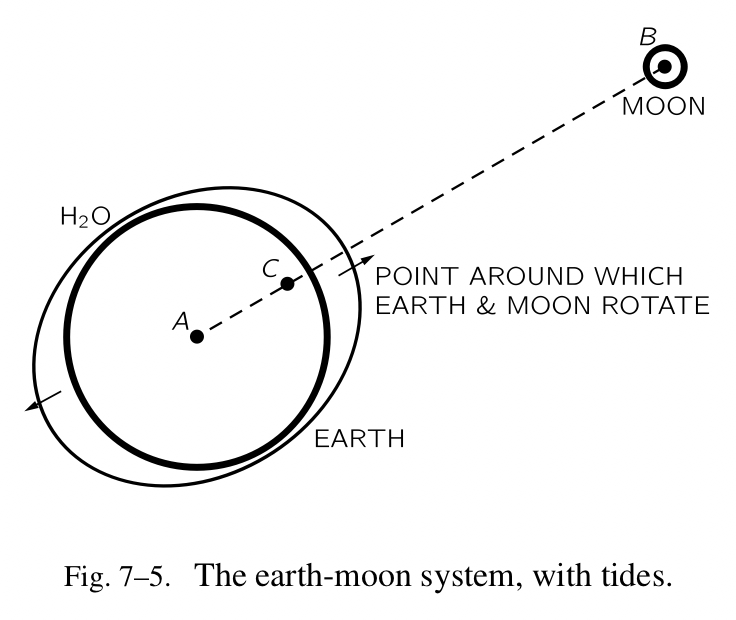
我们这里说的“被平衡”是什么意思？平衡了什么？如果月亮拉着整个地球朝向它，为什么地球没有向着月亮坠落？因为地球采用了和月亮一样的策略，它绕着一个点做环形运动，这个点在地球里面，但是不在其中心。月亮不仅仅围绕地球运动，地球和月亮都围绕一个中心位置运动，彼此的坠落都朝向这个共同点，正是如图 7-5 所示的 C 点。围绕共同中心的运动平衡了彼此的坠落。所以地球没有沿着直线走，而是做着环形运动。在远端的水是“未平衡的”，因为月亮的吸引力在那里更弱，相较于它在地球的中心点，在这里它正好平衡了“离心力”。这个不平衡的结果导致了水的升起，远离了地球的中心。在近端，来自月亮的吸引力更强，不平衡体现在相反的空间方向上，但是它再次远离了地球的中心。结论是我们得到了两个 tidal bulges。