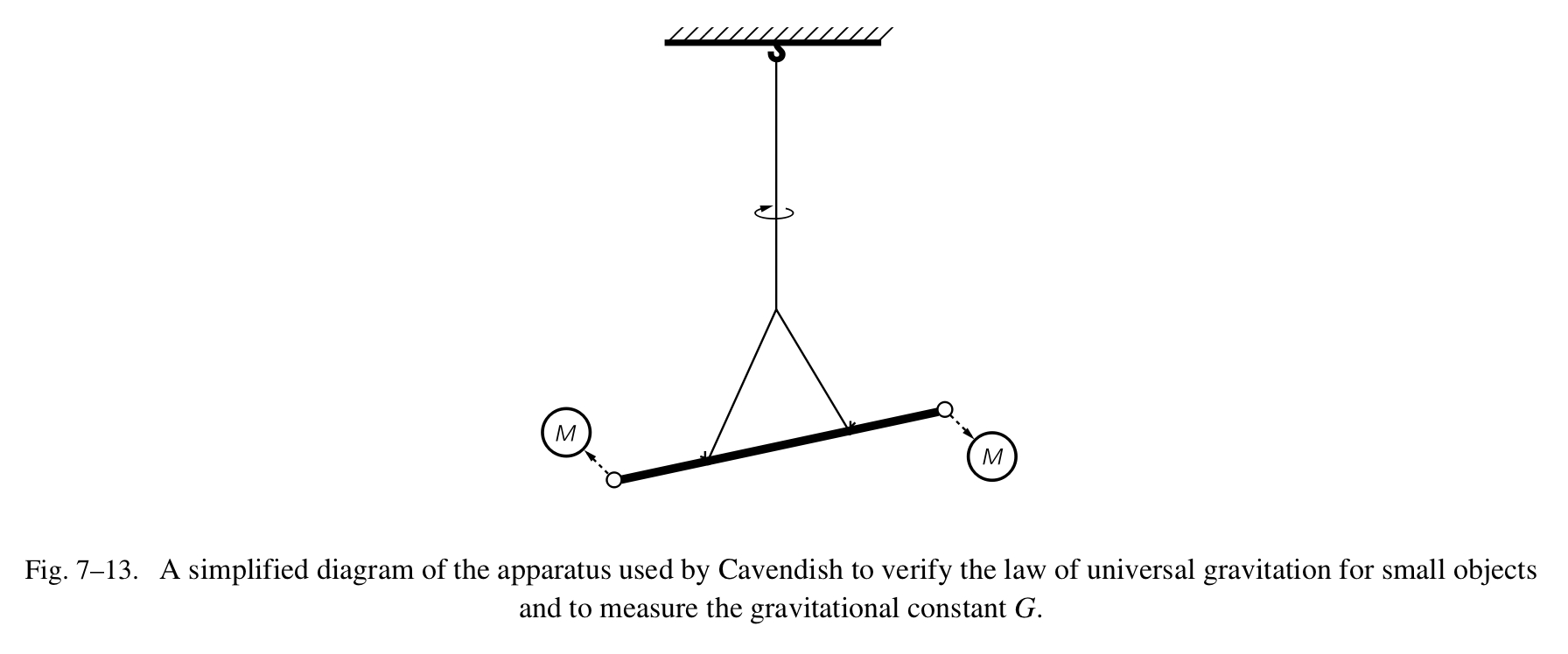
引力，它会延伸到很远的距离。如果在任意结对的物体之间存有一个力，那么我们应该可以测量它才对。不需要观察星球彼此的运动，为什么我们不拿一个铅球和一块大理石，然后观察大理石朝向铅球的运动呢？用这种简单的方式做实验会遭遇的困难是这个力非常的微弱。必须要很细心，比如要让设备隔离空气，不要让其带电，等等；然后力就能被测出来。第一个测算的人是卡文迪什，他的设备的简化图解如 Fig.7-13 所示。他首次阐明了在两个大的、固定的铅球和两个位于一个细杆两端的小的铅球之间的力，细杆也被称为扭力杆。通过测量细杆是如何扭动的，我们可以测量力的强度，验证其是否与距离的平方成反比，进而得出它的大小。因此我们也许可以精确地定义公式中的系数 G 。

\[F=G\frac{mm'}{r^2}\]

所有的质量和距离都是已知的。你说，“我们对地球已经瞭如指掌。”确实，但是我们还不知晓地球的质量。通过这个实验了解 G，并且了解地球的吸引力有多强，我们可以间接知道地球的质量到底有多大！有人把这个实验叫作“称量地球”，它可以被用来定义引力定律的系数 G 。这是定义地球质量的唯一方式。G 被算出来是：

\[6.670\times{10^{-11}newton\cdot{m^2}/kg^2}\]

很难估量引力理论的巨大成功在科学的历史上产生的影响有多大。早期流行的观点让人困惑，缺少自信，这些不完整的知识引来永不停歇的争执和悖论，相较之下，这条理论清晰、简明——事实上所有的卫星、行星以及星球都被这个简单的规则所主宰，人类可以更进一步地理解它，然后推导出行星的运动！这就是为什么科学接下来会成功，因为它给了大家希望，也许世界上的其他现象也会存在着如此美丽、简明的定律。