在等式（9.4）中，我们把速度分解成部分，告知物体在 x-方向、y-方向和 z-方向上是如何移动的。如果我们给出它的三个矩形部分的数值，速度就能被完整的阐释，包含数值和方向：

\[v_x=dx/dt\] \[v_y=dy/dt\] \[v_z=dz/dt\]

换句话说，物体的速度是

\[ds/dt=|v|=\sqrt{v_x^2+v_y^2+v_z^2}\]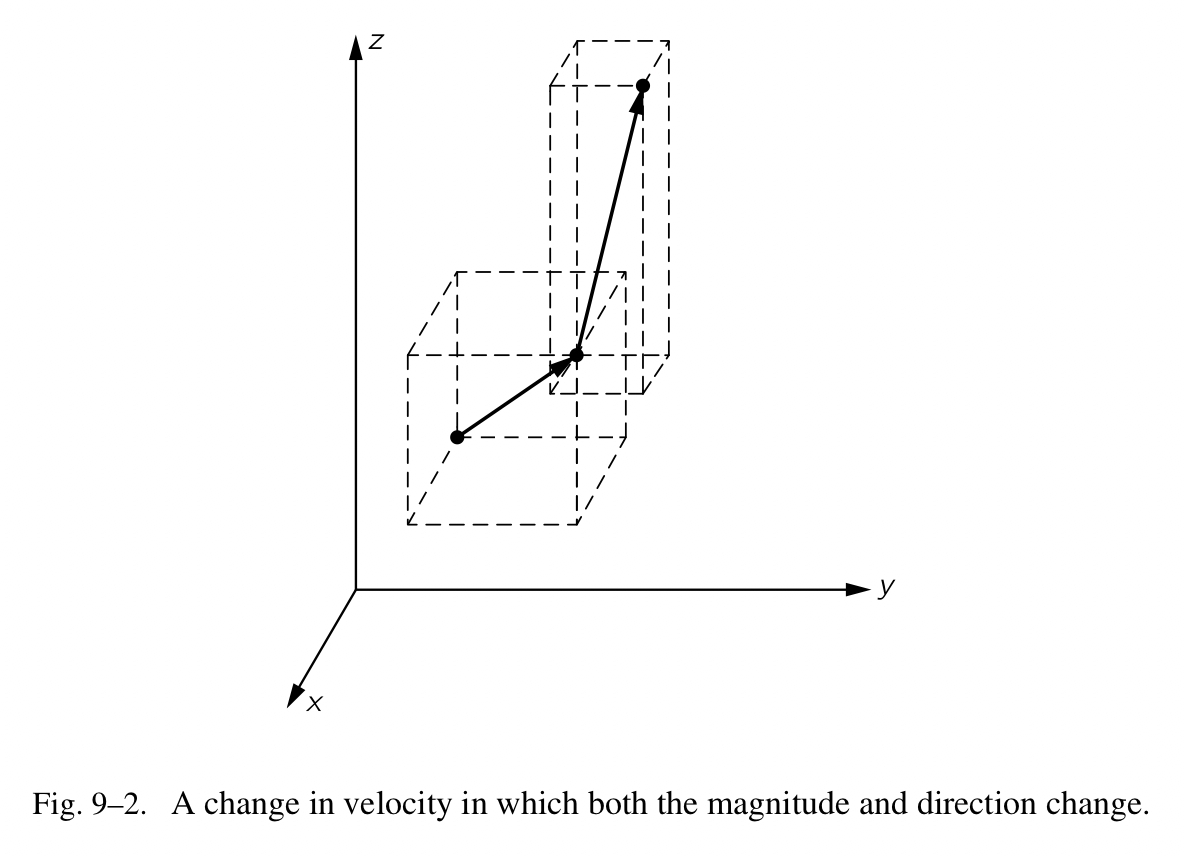

接下来，可能由于力的作用，速度变化成其他的方向和不同的数值，如图 Fig.9-2 所示。如果我们可以估算在速度的 x-、y-、z-部分上的变化，我们就能相当容易地分析看起来蛮复杂的情形。在时间 $\Delta{t}$ 内的 x-方向上的速度部分的改变是 $\Delta{v_x}=a_x\Delta{t}$ ，这儿的 $a_x$ 我们称之为加速度的 x-部分。相似的，我们会看到 $\Delta{v_y}=a_y\Delta{t}$ 和 $\Delta{v_z}=a_z\Delta{t}$ 。在这些术语中，我们看到牛顿第二定律说力的方向与加速度一致，这真的是三条定律，因为在 x-、y-、z-方向上的力的部分等于质量乘以对应的速度部分的变化比率：

eq-9-7

\[F_x=m(dv_x/dt)=m(d^2x/dt^2)=ma_x\] \[F_y=m(dv_y/dt)=m(d^2y/dt^2)=ma_y\] \[F_z=m(dv_z/dt)=m(d^2z/dt^2)=ma_z\]

和速度一样，通过投射表示某个数值的一条线段，加速度也可以被分解成部分，它的方向坐落在三个坐标轴上，所以，同样的，在一个给定方向上的力可以表示成在 x-、y-、z-方向上的确定的部分：

\[F_x=F \cos(x, F)\] \[F_y=F \cos(y, F)\] \[F_z=F \cos(z, F)\]

其中 F 是力的大小，（x, F）表示 x-轴和 F 方向的夹角，等等。

牛顿第二定律在等式（eq.9.7） 中被完整地展示。如果我们知道在一个物体上的作用力，然后将其拆分成 x-、y-、z-部分，我就能通过这些等式求得该物体的运动。如果在 y-、z-方向上没有作用力，力仅仅作用在 x-方向上，我们说，它是垂直的。等式（eq.9.7）告诉我们在垂直方向上的力会发生变化，但是在水平方向上不会改变。这些曾被第7章的一个特殊装置描述过（如图 Fig.7-3 所示）。一个正在坠落的物体在水平方向上不会发生任何改变，同时它在垂直方向上的运动跟假定其水平运动为 0 的自由落体并无二致。换句话说，如果这些力不相关，在 x-、y-、z-方向上的运动是独立的。