现在让我们真地求解。假设我们采纳 $\epsilon=0.100$ 秒。在我们做了所有工作之后，如果我们发现其不够小，我们也许不得不返回去，再以 $\epsilon=0.010$ 秒做一次。以我们的初始值 $x(0)=1.00$ 开始， $x(0.1)$ 是什么？它是旧的位置 $x(0)$ 加上速度（为 0）乘以 0.10 秒。因此 $x(0.1)$ 仍然是 1.00 因为它还没有开始移动。但是在 0.10 秒的新的速度是旧的速度 $v(0)=0$ 加上 $\epsilon$ 乘以加速度。加速度是 $-x(0)=-1.00$ 。那么

\[v(0.1)=0.00-0.10\times{1.00}=-0.10\]

在 0.2 秒处：

\[x(0.2)=x(0.1)+\epsilon{v(0.1)}=1.00-0.10\times{0.10}=0.99\]

以及

\[v(0.2)=v(0.1)+\epsilon{a(0.1)}=-0.10-0.10\times{1.00}=-0.20\]

诸如此类，我们可以计算剩余的运动。然而，为了达成特定的目标，有一些小的技巧可以提高精度。如果我们沿用这种计算，我们会发现运动相当的粗糙，因为 $\epsilon=0.100$ 秒并不精确，或许我们会采纳一个非常小的间隔，比如， $\epsilon=0.01$ 。选择一个合适的时间间隔将会花掉大量的计算循环。所以我们应该组织一下工作，提升我们的计算精度，但依旧使用这个粗糙的间隔 $\epsilon=0.10$ 秒。如果我们可以在这个分析技术中做一个微小的改动，它就可以实现。

注意新的位置是旧的位置加上时间间隔 $\epsilon$ 乘以速度。但是是什么时候的速度呢？在时间间隔的伊始是一种速度，在时间间隔的结束又是另一种速度。我们的改动是使用介于中间的速度。如果我们知道当前的速率，但是速率是一直变化的，通过使用跟当前一致的速率我们并不会得到正确的答案。我们应该使用介于“当前”速率和在时间间隔结尾的“那时”速率之间的某个速率。相同的思考也会应用到速度：为了计算速度的改变，我们应该使用位于两个时间的中间点上的加速度（在这两个时间上的速度被我们采纳）。所以我们的等式将会是这个样子：稍后的位置等于之前的位置加上 $\epsilon$ 乘以在间隔中间的时间上的速度。相似的，在这个中间点的速度是在之前的一个时间 $\epsilon$ 的速度（该时间是之前间隔的中间值）加上 $\epsilon$ 乘以在时间 t 的加速度。公式被写作：

eq-9-16

\[x(t+\epsilon)=x(t)+\epsilon{v(t+\epsilon{/2})}\] \[v(t+\epsilon{/2})=v(t-\epsilon{/2})+\epsilon{a(t)}\] \[a(t)=-x(t)\]

现在仅剩一个小问题： $v(\epsilon{/2})$ 是什么？起初，我们给定的是 $v(0)$ ，而非 $v(-\epsilon{/2})$ 。为了让我们开始，我们会使用一个特别的等式， $v(\epsilon{/2})=v(0)+(\epsilon{/2})a(0)$

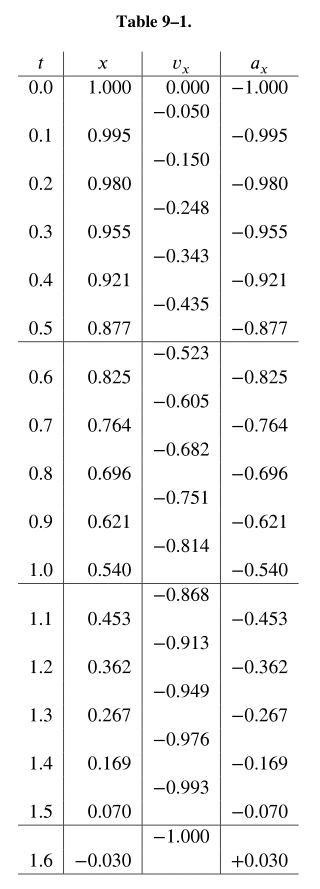
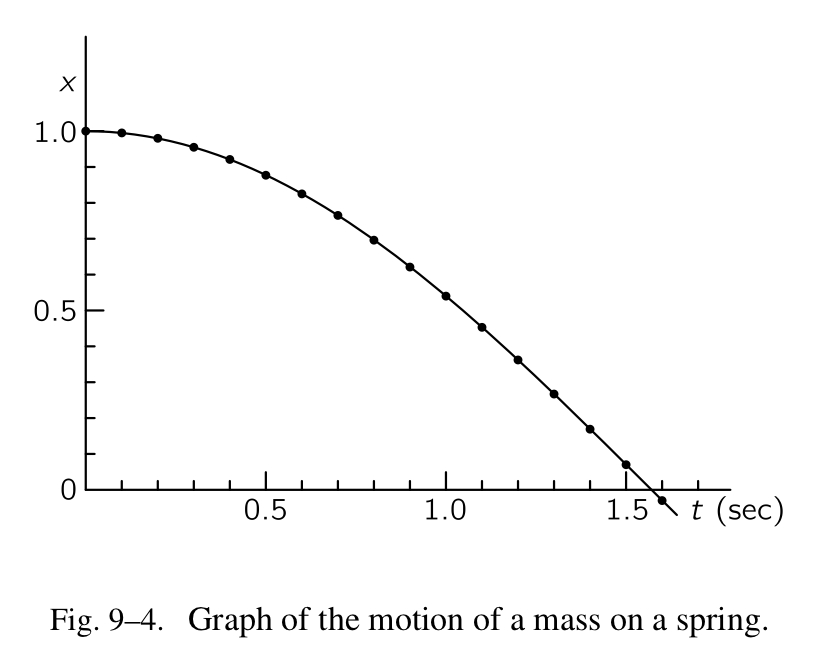
现在我们已经准备好完成我们的计算。我们或许可以以一种表格的形式组织我们的工作，其中的列是时间、位置、速度、加速度以及介于各行之间的速度，如表格 9-1 所示。当然，像这样的表格仅仅是一种表示数值的便捷的方式，这些数值是由一系列的等式获得的（eq.9.16），实际上，这些等式根本不需要写出来。我们只需要一个接一个的填充好表格。这个表格揭示了有关运动的一个很棒的点子：它从静止开始，起初获得了一点向上的（负的）速度，并且丢失了一些距离。然后加速度会变得稍小一些，但是会持续地获得速率。随着它的行径，速率会缓慢地变得越来越大，直到它通过了 $x=0$ ，大概在 $t=1.50$ 秒处，我们可以自信地预测它将会继续移动，只不过现在它会在另外一边；位置 x 会变成负的，加速度会变成正的。所以速率会减小。将这些数字与函数 $x=\cos(t)$ 比较会很有趣，如图 Fig.9-4 所示。它们完全匹配三位有效数字的精度！晚点我们应该会看到 $x=\cos(t)$ 就是我们运动等式的正确的数学之解，这个数值型分析的阐述让人印象深刻，没想到一个简单的计算能够给出如此精确的结果。