上面对于弹簧的振动的分析非常棒，但是我们可以分析一个围绕着太阳的行星的运动吗？让我们看看我们是否可以使用近似椭圆的轨道。我们应该假设太阳非常重，也就是说我们不应该涉及它的运动。如果一个行星在一个确定的地方启动，并且以一个确定的速度移动；它绕着太阳沿着某种曲线运动，我们会尝试分析，通过牛顿的运动定律和他的引力定律，是什么样的曲线？在给定的一个时刻，它位于空间中的某个位置。如果从太阳到该位置的半径的距离被叫做 r ，然后我们知道有一个向内的作用力，根据引力定律，它等于一个常数乘以太阳的质量和行星的质量的乘积除以距离的平方。为了进一步分析，我们必须要搞清楚什么样的加速度会由这个作用力产生出来。我们需要加速度沿着两个方向的部分，我们称之为 x 和 y 。因此如果我们可以通过给出 x 和 y （我们应该假设 z 总是 0 ，因为在 z-方向上没有作用力，如果没有初始的速度 $v_x$ ，就不会产生 z 。）明确行星在给定的一个时刻的位置，作用力会导向连接着行星和太阳的线。

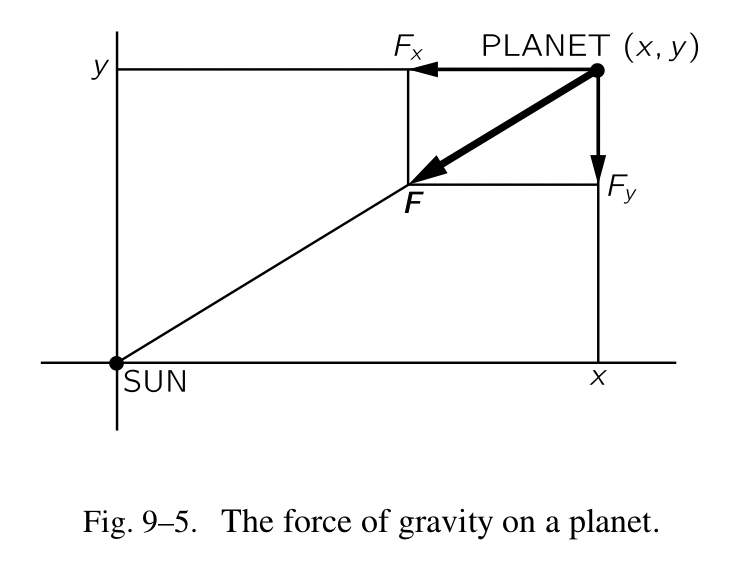
从上图可以看出，作用力的水平部分关联整个作用力，就像水平的距离 x 关联整个斜边 r 一样，因为这两个三角形是相似的。如果 x 是正的， $F_x$ 就是负的。 $F_x/\lvert F\rvert=-x/r$ or $F_x=-\lvert F\rvert x/r=-GMmx/r^3$ 。现在我们使用动态定律求得这个作用力的部分等于行星的质量乘以它的速度在 x-方向上的变化率。因此我们得到下面的定律：

eq-9-17

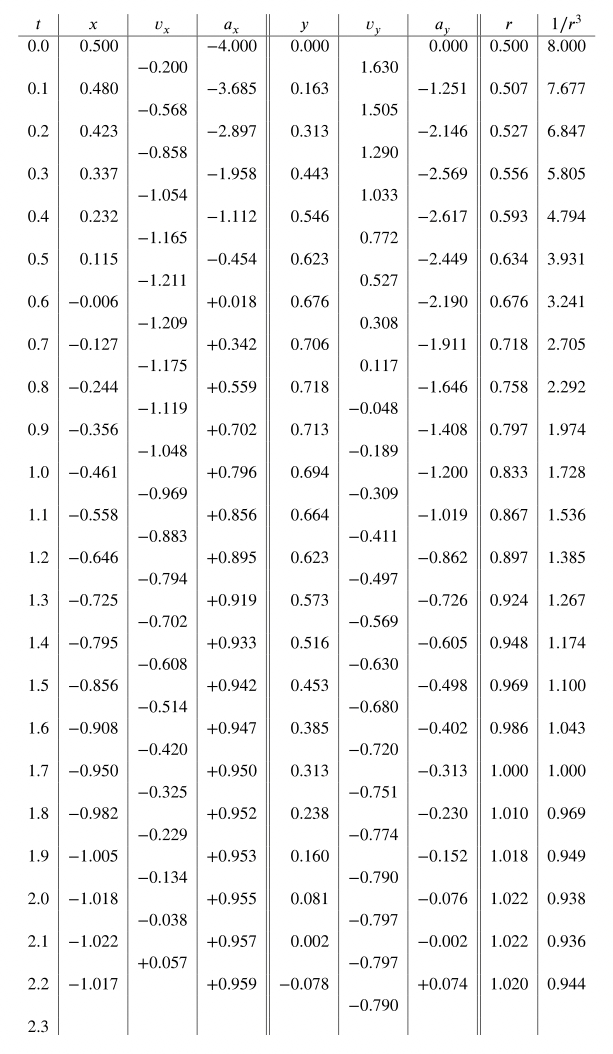
\[m(dv_x/dt)=-GMmx/r^3\] \[m(dv_y/dt)=-GMmy/r^3\] \[r=\sqrt{x^2+y^2}\]

这就是接下来我们必须要解决的一系列的等式。为了简化数值型的工作，我们假设时间的单位，或者太阳的质量已经被调整过，得到 $GM=1$ ，对于该例子，我们会假设行星的初始位置是在 $x=0.500$ 和 $y=0.00$ 处，并且最开始的速度全部在 y-方向上，它的数值是 1.630 。那么我们该如何计算呢？我们再搞一个表格，它的列是时间、x-位置、x-速度 $v_x$ 以及 x-加速度 $a_x$ ；接下来被一个双划线分开，另外三个列是在 y-方向上的位置、速度以及加速度。为了得到加速度，我们需要等式 eq.9.17；它告诉我们在 x-方向上面的加速度是 $-x/r^3$ ，在 y-方向上面的加速度是 $-y/r^3$ ，以及 r 是 $x^2+y^2$ 的平方根。因此给定 x 和 y ，我们必须要做一点计算，求得 r 之后我们就能计算两个加速度，再算出 $1/r^3$ 。如果使用平方表、立方表以及倒数表，这个工作会变得非常简单。

我们的计算可以继续下去，使用时间间隔 $\epsilon =0.100$ ：初始值位于 $t=0$ 处：

\[x(0)=0.500\quad y(0)=0.000\] \[v_x(0)=0.000\quad v_y(0)=+1.630\]

由这些我们可以得到：

\[r(0)=0.500\quad 1/r^3=8.000\] \[a_x=-4.000\quad a_y=0.000\]

因此我们可以计算速度 $v_x(0.05)$ 和 $v_y(0.05)$ ：

\[v_x(0.05)=0.000-4.00\times{0.050}=-0.200\] \[v_y(0.05)=1.630+0.000\times{0.050}=1.630\]

现在我们主要的计算开始了：

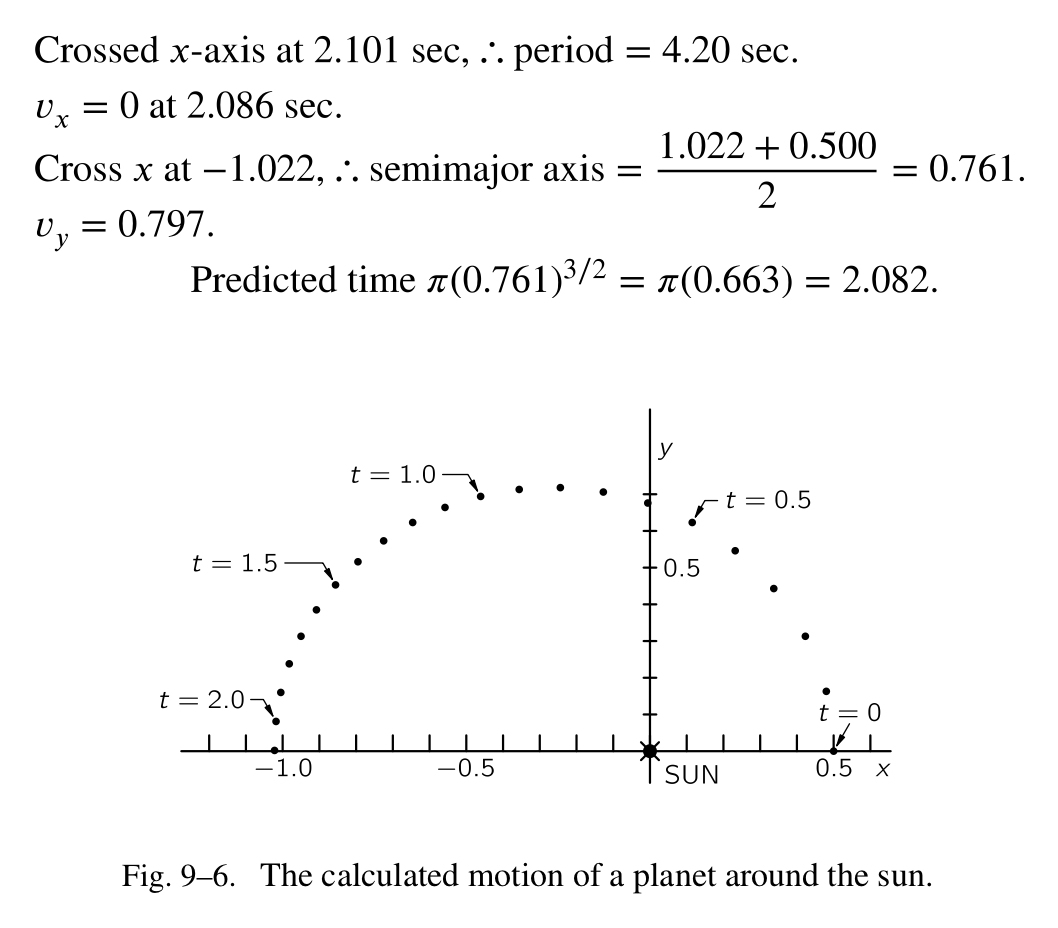
\[x(0.1)=0.500-0.200\times{0.100}=0.480\] \[y(0.1)=0.0+1.630\times{0.100}=0.163\] \[r=\sqrt{0.480^2+0.163^2}=0.507\] \[1/r^3=7.677\] \[a_x(0.1)=-0.480\times{7.677}=-3.685\] \[a_y(0.1)=-0.163\times{7.677}=-1.250\] \[v_x(0.15)=-0.200-3.685\times{0.100}=-0.568\] \[v_y(0.15)=1.630-1.250\times{0.100}=1.505\] \[x(0.2)=0.480-0.568\times{0.100}=0.423\] \[y(0.2)=0.163+1.505\times{0.100}=0.313\] \[...\]

通过这种方式，我们得到了表格 9-2，历经差不多 20 个步骤，我们描绘出了行星围绕太阳运动的一半！在图形 9-6 中给出了 x- 和 y-坐标点，它们对应于表格 9-2。这些点表示在连续的单位的十分之一的时间处的位置；我们看到最初行星移动地很快，在结尾处它移动地缓慢，曲线的形状被确定下来。因此我们可以看到，我们真地知道该如何计算行星的运动！

table-9-2

现在让我们看看我们该如何计算海王星、木星、天王星或者任意的其他行星。如果我们有非常多的行星，并且太阳也在移动，我们还能做相同的事情吗？当然没有问题。我们会计算作用在一个特定行星上的力，让我们说行星（编号）i ，有一个位置 $x_i$ , $y_i$ , $z_i$ （i=1 也许表示的是太阳，i=2 表示水星，i=3 表示金星，等等），我们必须要知道所有行星的位置。作用在一个上的力是由所有其他的物体导致的，它们的位置是 $x_j$ , $y_j$ , $z_j$ 。等式可以写作：

eq-9-18

\[m_i\frac{dv_{ix}}{dt}=\sum_{j=1}^N-\frac{Gm_im_j(x_i-x_j)}{r_{ij}^3}\] \[m_i\frac{dv_{iy}}{dt}=\sum_{j=1}^N-\frac{Gm_im_j(y_i-y_j)}{r_{ij}^3}\] \[m_i\frac{dv_{iz}}{dt}=\sum_{j=1}^N-\frac{Gm_im_j(z_i-z_j)}{r_{ij}^3}\]

更进一步，我们把 $r_{ij}$ 定义为介于两个行星 i 和 j 之间的距离；它等价于：

eq-9-19

\[r_{ij}=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2+(z_i-z_j)^2}\]

$\sum$ 表示所有 j 的值的和——所有其他的物体，除了 $j=i$ 。因此我们需要做的是弄更多的列。为了木星，我们需要 9 个列，为了土星，我们需要 9 个，等等。当我们有了所有的初始位置和速度，我们就能计算出所有的加速度，先使用等式 eq.9.19 计算所有的距离，再使用等式 eq.9.18。做这些需要花费多长时间？如果你在家里做的话，将会花费非常长！但是现在我们有机器能够非常迅速地处理这些运算；一个非常棒的计算机或许会花费 1 微秒，也就是 1 秒的百万分之一，去做一个加法。做乘法会花费更长的时间，10 微秒。在一个计算循环里，我们也许有 30 个乘法，或者与之类似的，所以一个循环将会花费 300 微妙。这也就意味着我们每秒能做 3000 个计算的循环。为了更加精确，比如到十亿分之一，我们需要 $4\times{10^5}$ 个循环去匹配行星围绕太阳做一次环形运动。它对应的计算时间是 130 秒，大约两分钟。因此追踪木星环绕太阳仅仅需要两分钟，所有行星的摄动精确到十亿分之一！（可以证明误差大概是随着间隔 $\epsilon$ 的平方发生改变。如果把间隔缩小 1,000 倍，那么它会精确 1,000,000 倍。所以，让我们把间隔缩小 10,000 倍。）

正如我们所说，在章节伊始我们甚至不知道该如何计算在一个弹簧上的质量的运动。现在，借助牛顿定律的伟大之力，我们不仅仅可以计算如此简单的运动，而且使用一个能够处理运算的机器，即使是极其复杂的行星的运动，也可以如我们所愿，达到很高的精度。